Main Article Content
Abstract
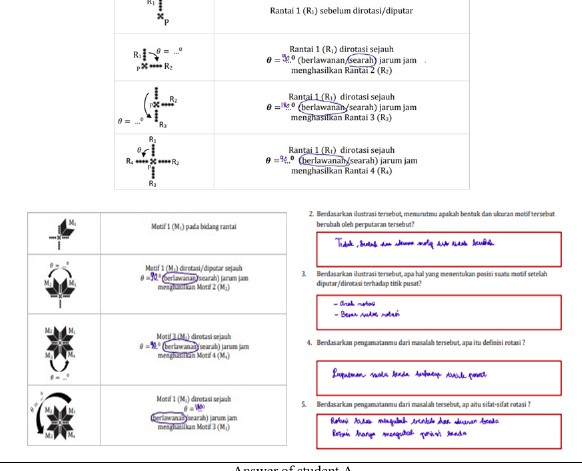
Rotation (rotation) is one of the materials in the transformation of geometry. Rotational learning can be the basis for student understanding geometrically because of its dynamic nature. Rotational learning can allow students to relate some geometric concepts such as congruence and equivalence. The study aims to explore the students’ inductive reasoning in rotation problem through the context of songket Palembang pattern in class. This research is related to the Indonesian Realistic Mathematics Approach (PMRI) as a learning approach used. The methodology used in this study is Design Research type validation studies consisting of three stages: preliminary design, experimental design, and retrospective analysis. The study was conducted for IX grade students of SMP Negeri 1 Palembang. The learning path (Hypothetical Learning Trajectory) in design research plays an important role as a research design and instrument. The Hypothetical Learning Trajectory was developed together with a series of activities using the contet of songket Palembang pattern such as pucuk rebung pattern, lepus pattern, lintang pattern, etc. Data collected in the form of video recordings and photos during the learning process, student interviews, student work results, discussion results, and field notes at each meeting. The instruments used include documentation in the form of video recordings and photos, interview sheets, student activity sheets, field note sheets, and the Hypothetical Learning Trajectory (HLT). Media used in this study was the students’ worksheet. The result of this study indicated that exploration using the context of songket Palembang patterns can help inductive reasoning ability on students when solving rotation problem. The conclusion of this study is the use of songket Palembang pattern as starting point in mathematics learning in rotation material helps the students to explore their inductive reasoning skill in solving rotation problems.
DOI : https://doi.org/10.22342/jpm.16.1.14304.57-72
Keywords
Article Details
Copyright (c) 2022 Arika Sari, Ratu Ilma Indra Putri

This work is licensed under a Creative Commons Attribution 4.0 International License.
This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.
All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).
References
- Bakker, A. (2018). Design research in Education: A Practical Guide for Early Career Researchers. London: Routledge.
- Bansilal, S., James, A., & Naidoo, M. (2014). Whose voice matters? LEARNERS. South African Journal of Education, 30(1), 153 - 165. https://doi.org/10.15700/saje.v30n1a236.
- de Villiers, M. (2017). An explanatory, transformation geometry proof of a classic treasure-hunt problem and its generalization. International Journal of Mathematical Education in Science and Technology, 48(2), 260–267. https://doi.org/10.1080/0020739X.2016.1210245
- Edwards, L. D. (1997). Exploring the territory before proof: students’ generalizations in a computer microworld for transformation geometry. International Journal of Computers for Mathematical Learning 2, 187–215. https://doi.org/10.1023/A:1009711521492.
- Febriani, C., & Rosyidi, A. H. (2013). Identification of Students' Inductive Reasoning in Solving Mathematical Problems [in Bahasa]. Mathedenusa Journal, 2(1). https://doi.org/10.26740/mathedunesa.v2n1.
- Karen F Hollebrands. (2003). High school students’ understandings of geometric transformations in the context of a technological environment. The Journal of Mathematical Behavior, Volume 22, Issue 1, Pages 55-72. https://doi.org/10.1016/S0732-3123(03)00004-X
- Kemendikbud. (2018). Buku Guru Matematika Kelas IX SMP. Jakarta: Kemendikbud.
- Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics.
- Boston: TIMSS & PIRLS International Study Center.
- Morris, T. & Paulsen, R. (2011). Using Tracing Paper to Teach Transformation Geometry.
- Johannensberg: Amesa.Naidoo, J. & Bansilal, S. (2010). Strategies Used by Grade 12 Mathematics Learners in Transformation Geometry.
- Proceedings of the eighteenth annual meeting of the Southern African association for research in mathematics, science, and technology education, 182–190. University of KwaZulu-Natal: South Africa.
- Nasution, M. F., Putri, R. I. I., & Zulkardi. (2018). Rowing sport in learning fractions of the fourth grade students. Journal on Mathematics Education, 9(1), 69-80. https://doi.org/10.22342/jme.9.1.4270.69-80.
- Putri, R. I. I., Dolk, M., & Zulkardi. (2015). Professional development of PMRI teachers for introducing social norms. Journal on Mathematics Education, 6(1), 11-19. https://doi.org/10.22342/jme.6.1.1900.11-19.
- Putri, R. I. I. & Zulkardi. (2018). Learning fraction through the context of Asian Games 2018. Journal of Physics: Conference Series, 1088(1), 1-8. https://doi.org/10.1088/1742- 6596/1088/1/012023.
- Panorkou, N. & Maloney A. (2015) Elementary students’ construction of geometric transformation reasoning in a dynamic animation environment. Constructivist Foundations 10(3), 338–347. http://constructivist.info/10/3/338.
- Schultz, K. A. & Austin, J. D. (1983). Directional effect in transformation tasks. Journal Research in Mathematics Education, 14(2), 95 - 101. https://doi.org/10.5951/jresematheduc.14.2.0095.
- Soegeng, T. (1983). Get to know Indonesian Ornamental Variety [in Bahasa]. Surakarta: Aski Sub- Project IKI Development Project.
- Thaqi, X., & Gimenez, J. (2012). Prospective teacher’s understanding of geometric transformation. Proceedings in 12th International Congress on Mathematical Education ICME12, 8 - 15. Seoul, Korea.
- Trung, N., Thao, T., Tran, T. (2019). Realistic mathematics education (RME) and didactical situations in mathematics (DSM) in the context of education reform in Vietnam. Journal of Physics: Conference Series, 1340. http://dx.doi.org/10.1088/1742-6596/1340/1/012032
- Utari, Rahma Siska & Indra Putri, Ratu & Hartono, Yusuf. (2015). The Palembang Cultural Context to Support the Reasoning Ability of Middle School Students on Comparative Materials. Mathematics Didactic Journal [in Bahasa]. 2. 27- .https://www.researchgate.net/publication/347487990
- Van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic Mathematics Education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 521–525). Dordrecht: Springer
- Yansen, D., Putri, R. I. I., Zulkardi & Fatimmah, S. (2019). Developing PISA-like mathematics problem on uncertainty and data using the Asian Games football context. Journal on Mathematics Education, 10(1): 37-46. https://doi.org/10.22342/jme.10.1.5249.37-46.
- Zainab, Zulkardi & Yusuf. (2013). Learning Design of Number Pattern Material with PMRI Approach Using Traditional Crafts of Palembang Tajung Fabrics for Class IX SMP [in Bahasa]. Journal of Mathematics Education (EDUMAT), 4(7), 467 – 478.
- Zaini, A., & Marsigit. (2014). Comparison of the effectiveness of learning mathematics with realistic and conventional mathematics approaches in terms of students' mathematical reasoning and communication abilities [in Bahasa]. Journal of Mathematics Education Research, 1(2), 152- 163. https://doi.org/10.21831/jrpm.v1i2.2672.
- Zulkardi. (2002). Developing A Learning Environment on Realistic Mathematics Education for Indonesian Student Teachers. Published Dissertation. Enschede: University of Twente.
- Zulkardi & Putri, R. I. I. (2019). New School Mathematics Curricula, PISA and PMRI in Indonesia. In Lam T.T. et.al (Eds) School Mathematics Curricula: Asian Perspectives and Glimpses of Reform. Singapore: Springer.
- Zulkardi, Putri, R.I.I, Widjaya, A. (2019). Two decades of Realistic Mathematics Education in Indonesia. In Panhuizen, M. (Eds.). International Reflections on the Netherlands Didactics of Mathematics: Visions on and Experiences with Realistic Mathematics Education (ICME-13 Monographs). Netherlands: Springer.
References
Bakker, A. (2018). Design research in Education: A Practical Guide for Early Career Researchers. London: Routledge.
Bansilal, S., James, A., & Naidoo, M. (2014). Whose voice matters? LEARNERS. South African Journal of Education, 30(1), 153 - 165. https://doi.org/10.15700/saje.v30n1a236.
de Villiers, M. (2017). An explanatory, transformation geometry proof of a classic treasure-hunt problem and its generalization. International Journal of Mathematical Education in Science and Technology, 48(2), 260–267. https://doi.org/10.1080/0020739X.2016.1210245
Edwards, L. D. (1997). Exploring the territory before proof: students’ generalizations in a computer microworld for transformation geometry. International Journal of Computers for Mathematical Learning 2, 187–215. https://doi.org/10.1023/A:1009711521492.
Febriani, C., & Rosyidi, A. H. (2013). Identification of Students' Inductive Reasoning in Solving Mathematical Problems [in Bahasa]. Mathedenusa Journal, 2(1). https://doi.org/10.26740/mathedunesa.v2n1.
Karen F Hollebrands. (2003). High school students’ understandings of geometric transformations in the context of a technological environment. The Journal of Mathematical Behavior, Volume 22, Issue 1, Pages 55-72. https://doi.org/10.1016/S0732-3123(03)00004-X
Kemendikbud. (2018). Buku Guru Matematika Kelas IX SMP. Jakarta: Kemendikbud.
Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics.
Boston: TIMSS & PIRLS International Study Center.
Morris, T. & Paulsen, R. (2011). Using Tracing Paper to Teach Transformation Geometry.
Johannensberg: Amesa.Naidoo, J. & Bansilal, S. (2010). Strategies Used by Grade 12 Mathematics Learners in Transformation Geometry.
Proceedings of the eighteenth annual meeting of the Southern African association for research in mathematics, science, and technology education, 182–190. University of KwaZulu-Natal: South Africa.
Nasution, M. F., Putri, R. I. I., & Zulkardi. (2018). Rowing sport in learning fractions of the fourth grade students. Journal on Mathematics Education, 9(1), 69-80. https://doi.org/10.22342/jme.9.1.4270.69-80.
Putri, R. I. I., Dolk, M., & Zulkardi. (2015). Professional development of PMRI teachers for introducing social norms. Journal on Mathematics Education, 6(1), 11-19. https://doi.org/10.22342/jme.6.1.1900.11-19.
Putri, R. I. I. & Zulkardi. (2018). Learning fraction through the context of Asian Games 2018. Journal of Physics: Conference Series, 1088(1), 1-8. https://doi.org/10.1088/1742- 6596/1088/1/012023.
Panorkou, N. & Maloney A. (2015) Elementary students’ construction of geometric transformation reasoning in a dynamic animation environment. Constructivist Foundations 10(3), 338–347. http://constructivist.info/10/3/338.
Schultz, K. A. & Austin, J. D. (1983). Directional effect in transformation tasks. Journal Research in Mathematics Education, 14(2), 95 - 101. https://doi.org/10.5951/jresematheduc.14.2.0095.
Soegeng, T. (1983). Get to know Indonesian Ornamental Variety [in Bahasa]. Surakarta: Aski Sub- Project IKI Development Project.
Thaqi, X., & Gimenez, J. (2012). Prospective teacher’s understanding of geometric transformation. Proceedings in 12th International Congress on Mathematical Education ICME12, 8 - 15. Seoul, Korea.
Trung, N., Thao, T., Tran, T. (2019). Realistic mathematics education (RME) and didactical situations in mathematics (DSM) in the context of education reform in Vietnam. Journal of Physics: Conference Series, 1340. http://dx.doi.org/10.1088/1742-6596/1340/1/012032
Utari, Rahma Siska & Indra Putri, Ratu & Hartono, Yusuf. (2015). The Palembang Cultural Context to Support the Reasoning Ability of Middle School Students on Comparative Materials. Mathematics Didactic Journal [in Bahasa]. 2. 27- .https://www.researchgate.net/publication/347487990
Van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic Mathematics Education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 521–525). Dordrecht: Springer
Yansen, D., Putri, R. I. I., Zulkardi & Fatimmah, S. (2019). Developing PISA-like mathematics problem on uncertainty and data using the Asian Games football context. Journal on Mathematics Education, 10(1): 37-46. https://doi.org/10.22342/jme.10.1.5249.37-46.
Zainab, Zulkardi & Yusuf. (2013). Learning Design of Number Pattern Material with PMRI Approach Using Traditional Crafts of Palembang Tajung Fabrics for Class IX SMP [in Bahasa]. Journal of Mathematics Education (EDUMAT), 4(7), 467 – 478.
Zaini, A., & Marsigit. (2014). Comparison of the effectiveness of learning mathematics with realistic and conventional mathematics approaches in terms of students' mathematical reasoning and communication abilities [in Bahasa]. Journal of Mathematics Education Research, 1(2), 152- 163. https://doi.org/10.21831/jrpm.v1i2.2672.
Zulkardi. (2002). Developing A Learning Environment on Realistic Mathematics Education for Indonesian Student Teachers. Published Dissertation. Enschede: University of Twente.
Zulkardi & Putri, R. I. I. (2019). New School Mathematics Curricula, PISA and PMRI in Indonesia. In Lam T.T. et.al (Eds) School Mathematics Curricula: Asian Perspectives and Glimpses of Reform. Singapore: Springer.
Zulkardi, Putri, R.I.I, Widjaya, A. (2019). Two decades of Realistic Mathematics Education in Indonesia. In Panhuizen, M. (Eds.). International Reflections on the Netherlands Didactics of Mathematics: Visions on and Experiences with Realistic Mathematics Education (ICME-13 Monographs). Netherlands: Springer.