Main Article Content
Abstract
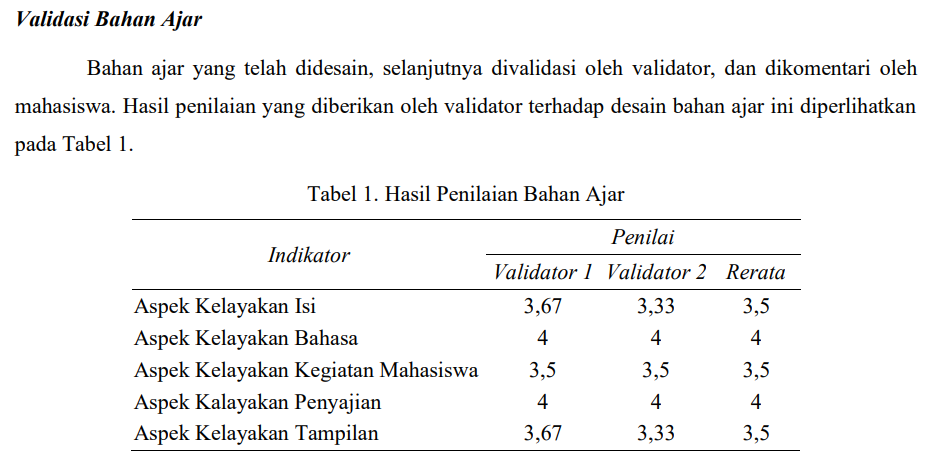
The article describes about validation of teaching material in which some probing-prompting questions were created to construct students’ understanding about function of two variables. This research is a design research and its type is development study. Data was collected by walk-through and documentation methods. The research produced the structure of questions to construct students’ understanding about some topics which are domain, range, contour plot or contour maps, surface, and level of curve of function of two variables, and the teaching material is supplemented by Geogebra application. The questions about topics of domain and range material are probed by topics of domain and range of function of one variable. The teaching material is valid.
Keywords
Article Details
Copyright (c) 2019 Hapizah, Somakim, M. Yusup

This work is licensed under a Creative Commons Attribution 4.0 International License.
This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.
All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).
References
- Akker, J.V.D., et.al. (2006). Educational design research. Tersedia: http://www.fi.uu.nl/publicatied/literatur/EducationalDesignREsearch.pdf.
- BNSP. (2007). Peraturan Menteri Pendidikan Nasional Republik Indonesia Nomor 41 Tahun 2007 Tentang Standar Proses. Jakarta: Badan Standar Nasional Pendidikan.
- Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.
- Hapizah. (2014). Analisis Materi Persamaan Diferensial melalui Strategi Probing-Prompting. Jurnal Penelitian dan Pembelajaran Matematika (JPPM), 7 (1).
- Jones, S. R. & Dorko, A. (2015). Students’ Generalizations of Single-Variable Conceptions of The Definite Integral to Multivariate Conceptions. In (Eds.) T. Fukawa-Connelly, N. Engelke Infante, K. Keene, and M. Zandieh. Proceedings of The 18th Annual Conference on Research in Undergraduate Mathematics Education, Pittsburgh, Pennsylvania.
- Kabael, T. (2011). Generalizing single variable functions to two-variables function, function machine and APOS. Educational Sciences: Theory & Practice, 11 (1).
- Kashefi, H., Zaleha, T., & Yudariah, M.Y. (2010). Obstacles in the learning of two-variable function through mathematical thinking approach. Procedia Sosial & Behavioral Sciences, 8, 173 - 180.
- Martinez-Planell, R. & Trigueros, G, M. (2012). Students’ understanding of the general notion of a function of two variables. Educational Studies in Mathematics, 81 (3), 365-384.
- Martinez-Planell, R. & Trigueros, G, M. (2009). Students’ Ideas on Function of Two-Variables: Domain, Range, and Representation. Proceeding of PME-NA, 5, 73 - 80.
- McGee, D. & Martines-Planell, R. (2014). A study of semiotic registers in the development of the definite integral of functions of two and three variables. International Journal of Science and Mathematics Education, 12, 883 – 916.
- Montiel, Vidakovich, & Kabael. (2008). Relationship between students’ understanding of function in certesian and polar coordinate systems. Investigations in Mathematics Learning, 1 (2), 52 - 70.
- Ranjit, S. (2015). How to Develop and Produce Simple Learning Materials with Limited Resources. Tersedia: www.accu.or.jp/pub/pdf0106/rpp25
- Serhan, D. (2015). Students’ understanding of the definite integral concept. International Journal of Research in Education and Science (IJRES), 1 (1), 84-88.
- Suherman, dkk. (2008). Strategi pembelajaran matematika kontemporer. Bandung: Universitas Pendidikan Indonesia.
- Tessmer, M. (1993). Planning and Conducting Formative Evaluations. Philadelphia: Kogan page.
- Tall, D. O., McGoven, M., & DeMarois, P. (2000). The Function Machine as A Cognitive Root for Building A Rich Concept Image of The Function Concept. Proceedings of PME-NA, 1, 247-254.
- Trigueros, G, M. & Martines-Planell, R. (2010). Geometrical representation in the learning of two variable functions. Educational Studies in Mathematics, 73, 3-19.
- Trigueros, G, M. & Martines-Planell, R. (2018). On Students’ Understanding of Riemann Sum of Integrals of Function of Two Variables. HAL Archives-Ouvertes. https://hal.archives.fr/hal-01849951.
References
Akker, J.V.D., et.al. (2006). Educational design research. Tersedia: http://www.fi.uu.nl/publicatied/literatur/EducationalDesignREsearch.pdf.
BNSP. (2007). Peraturan Menteri Pendidikan Nasional Republik Indonesia Nomor 41 Tahun 2007 Tentang Standar Proses. Jakarta: Badan Standar Nasional Pendidikan.
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.
Hapizah. (2014). Analisis Materi Persamaan Diferensial melalui Strategi Probing-Prompting. Jurnal Penelitian dan Pembelajaran Matematika (JPPM), 7 (1).
Jones, S. R. & Dorko, A. (2015). Students’ Generalizations of Single-Variable Conceptions of The Definite Integral to Multivariate Conceptions. In (Eds.) T. Fukawa-Connelly, N. Engelke Infante, K. Keene, and M. Zandieh. Proceedings of The 18th Annual Conference on Research in Undergraduate Mathematics Education, Pittsburgh, Pennsylvania.
Kabael, T. (2011). Generalizing single variable functions to two-variables function, function machine and APOS. Educational Sciences: Theory & Practice, 11 (1).
Kashefi, H., Zaleha, T., & Yudariah, M.Y. (2010). Obstacles in the learning of two-variable function through mathematical thinking approach. Procedia Sosial & Behavioral Sciences, 8, 173 - 180.
Martinez-Planell, R. & Trigueros, G, M. (2012). Students’ understanding of the general notion of a function of two variables. Educational Studies in Mathematics, 81 (3), 365-384.
Martinez-Planell, R. & Trigueros, G, M. (2009). Students’ Ideas on Function of Two-Variables: Domain, Range, and Representation. Proceeding of PME-NA, 5, 73 - 80.
McGee, D. & Martines-Planell, R. (2014). A study of semiotic registers in the development of the definite integral of functions of two and three variables. International Journal of Science and Mathematics Education, 12, 883 – 916.
Montiel, Vidakovich, & Kabael. (2008). Relationship between students’ understanding of function in certesian and polar coordinate systems. Investigations in Mathematics Learning, 1 (2), 52 - 70.
Ranjit, S. (2015). How to Develop and Produce Simple Learning Materials with Limited Resources. Tersedia: www.accu.or.jp/pub/pdf0106/rpp25
Serhan, D. (2015). Students’ understanding of the definite integral concept. International Journal of Research in Education and Science (IJRES), 1 (1), 84-88.
Suherman, dkk. (2008). Strategi pembelajaran matematika kontemporer. Bandung: Universitas Pendidikan Indonesia.
Tessmer, M. (1993). Planning and Conducting Formative Evaluations. Philadelphia: Kogan page.
Tall, D. O., McGoven, M., & DeMarois, P. (2000). The Function Machine as A Cognitive Root for Building A Rich Concept Image of The Function Concept. Proceedings of PME-NA, 1, 247-254.
Trigueros, G, M. & Martines-Planell, R. (2010). Geometrical representation in the learning of two variable functions. Educational Studies in Mathematics, 73, 3-19.
Trigueros, G, M. & Martines-Planell, R. (2018). On Students’ Understanding of Riemann Sum of Integrals of Function of Two Variables. HAL Archives-Ouvertes. https://hal.archives.fr/hal-01849951.