Main Article Content
Abstract
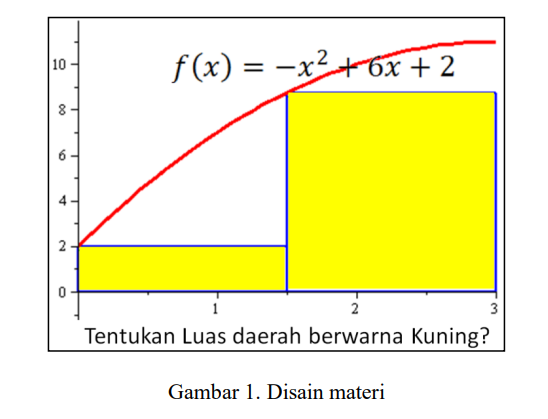
The aim of this study was to investigate the effect caused in learning of finite integral when a lecturer give a problem about finding area below a graph of the function with two partitions which the scale on Cartesian coordinate of x-axis different with y-axis. This research type was descriptively qualitative. The subject of this study was 32 undergraduate students majoring in mathematics education that attend integral calculus class at one universities in Palembang. In this study, the 32 students was formed become 6 groups. Instrument in this study was two problems that discussed by them in group. The data was collected by documentation of students’ worksheet, observation, and interview. The result showed the effect on students, that is, they seen try to construct their mathematics knowledge by themselves first, communicate unexpected ideas before, and can think critically on the given problem. The positive effects showed up because the given problem to them related with some concepts.
Keywords
Article Details
Copyright (c) 2019 Muhammad Win Afgani, Retni Paradesa

This work is licensed under a Creative Commons Attribution 4.0 International License.
This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.
All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).
References
- Afgani, M. W., Suryadi, D., & Dahlan, J. A. (2017). Analysis of undergraduate students’ mathematical understanding ability of the limit of function based on APOS theory perspective. Journal of Physics: Conference Series, 895, 012056.
- Afgani, M. W., Suryadi, D., & Dahlan, J. A. (2019). The enhancement of pre-service mathematics teachers' mathematical understanding ability through ACE teaching cyclic. Journal of Technology and Science Education, 9 (2), 153-167.
- Amalia, L. (2018). Pengembangan soal untuk mengukur kemampuan koneksi antar topik matematika siswa Sekolah Dasar. Jurnal Pendidikan Matematika RAFA, 3 (2), 195-216.
- Arifin, S. (2016). Penerapakn Pendekatan Contextual Teaching and Learning (CTL) untuk Melihat Kemampuan Komunikasi Matematis Mahasiswa Semester Awal Pendidikan Matematika UIN Raden Fatah. Jurnal Pendidikan Matematika RAFA, 2 (2), 142–160.
- Cavanagh, M., & Mitchelmore, M. (2003). Graphics calculators in the learning of mathematics: teacher understandings and classroom practices. Mathematics Teacher Education and Development, 5, 3-18.
- Hodiyanto. (2017). Kemampuan Komunikasi Matematis dalam Pembelajaran Matematika. AdMathEdu, 7 (1). 9-18.
- Kowiyah. (2012). Kemampuan Berpikir Kritis. Jurnal Pendidikan Dasar, 3 (5), 175-179.
- Larson, R. & Falvo, D. C. (2009). Calculus: An Applied Approach. USA: Brooks/Cole, Cengage Learning.
- Leinhardt, G., Zaslavsky, O., & Stein, M. K. (1990). Functions, Graphs, and Graphing: Tasks, Learning, and Teaching. Review of Educational Research, 60 (1), 1-64.
- Lloyd, M. & Bahr, N. (2010). Thinking critically about critical thinking in higher education. International Journal for the Scholarship of Teaching and Learning, 4 (2).
- Machaba, F. M. (2016). The concepts of area and perimeter: insights and misconceptions of grade 10 learners. Pythagoras: Journal of The Association for Mathematics Education of South Africa, 37 (1).
- Paradesa, R. (2015). Kemampuan berpikir matematis mahasiswa melalui pendekatan konstruktivisme pada mata kuliah matematika keuangan. Jurnal Pendidikan Matematika RAFA, 1 (2), 306-325.
- Paradesa, R., & Ningsih, Y. L. (2017). Pembelajaran matematika berbantuan maple pada mata kuliah kalkulus integral terhadap kemampuan komunikasi matematis mahasiswa. Jurnal Pendidikan RAFA, 3 (1), 70-81.
- Purcel, E. J. and Varberg, D. (1987). Calculus with analytic geometry, 5th Ed (Terjemahan: Susila, N., Kartasasmita, B. dan Rawuh). USA:Prentice-Hall. Inc.
- Rahmat, M. (2003). Modul geometri. Universitas Terbuka: Jakarta.
- Siagian, M. D. (2016). Kemampuan koneksi matematik dalam pembelajaran matematika. Journal of Mathematics Education and Science, 2 (1), 58-67.
- Su, H. F., Ricci, F. A., & Mnatsakanian, M. (2016). Mathematical teaching strategies: pathways to critical thinking and metacognition. Journal of Research in Education and Science (IJRES), 2 (1), 190-200.
- Sun, Y., Li, S., Bonini, N., & Liu, Y. (2016). Effect of graph scale on risky choice: evidence from preference and process in decision-making. PLoS ONE, 11 (1), e0146914.
- VanCleave, J. P. (1996). Gembira bermain dengan geometri: 101 percobaan yang pasti berhasil (Terjemahan: Pakar, D.). Pustaka Grafiti: Jakarta.
- Zaslavsky, O., Sela, H., & Leron, U. (2002). Being sloppy about slope: the effect of changing the scale. Educational Studies in Mathematics, 49, 119-140.
References
Afgani, M. W., Suryadi, D., & Dahlan, J. A. (2017). Analysis of undergraduate students’ mathematical understanding ability of the limit of function based on APOS theory perspective. Journal of Physics: Conference Series, 895, 012056.
Afgani, M. W., Suryadi, D., & Dahlan, J. A. (2019). The enhancement of pre-service mathematics teachers' mathematical understanding ability through ACE teaching cyclic. Journal of Technology and Science Education, 9 (2), 153-167.
Amalia, L. (2018). Pengembangan soal untuk mengukur kemampuan koneksi antar topik matematika siswa Sekolah Dasar. Jurnal Pendidikan Matematika RAFA, 3 (2), 195-216.
Arifin, S. (2016). Penerapakn Pendekatan Contextual Teaching and Learning (CTL) untuk Melihat Kemampuan Komunikasi Matematis Mahasiswa Semester Awal Pendidikan Matematika UIN Raden Fatah. Jurnal Pendidikan Matematika RAFA, 2 (2), 142–160.
Cavanagh, M., & Mitchelmore, M. (2003). Graphics calculators in the learning of mathematics: teacher understandings and classroom practices. Mathematics Teacher Education and Development, 5, 3-18.
Hodiyanto. (2017). Kemampuan Komunikasi Matematis dalam Pembelajaran Matematika. AdMathEdu, 7 (1). 9-18.
Kowiyah. (2012). Kemampuan Berpikir Kritis. Jurnal Pendidikan Dasar, 3 (5), 175-179.
Larson, R. & Falvo, D. C. (2009). Calculus: An Applied Approach. USA: Brooks/Cole, Cengage Learning.
Leinhardt, G., Zaslavsky, O., & Stein, M. K. (1990). Functions, Graphs, and Graphing: Tasks, Learning, and Teaching. Review of Educational Research, 60 (1), 1-64.
Lloyd, M. & Bahr, N. (2010). Thinking critically about critical thinking in higher education. International Journal for the Scholarship of Teaching and Learning, 4 (2).
Machaba, F. M. (2016). The concepts of area and perimeter: insights and misconceptions of grade 10 learners. Pythagoras: Journal of The Association for Mathematics Education of South Africa, 37 (1).
Paradesa, R. (2015). Kemampuan berpikir matematis mahasiswa melalui pendekatan konstruktivisme pada mata kuliah matematika keuangan. Jurnal Pendidikan Matematika RAFA, 1 (2), 306-325.
Paradesa, R., & Ningsih, Y. L. (2017). Pembelajaran matematika berbantuan maple pada mata kuliah kalkulus integral terhadap kemampuan komunikasi matematis mahasiswa. Jurnal Pendidikan RAFA, 3 (1), 70-81.
Purcel, E. J. and Varberg, D. (1987). Calculus with analytic geometry, 5th Ed (Terjemahan: Susila, N., Kartasasmita, B. dan Rawuh). USA:Prentice-Hall. Inc.
Rahmat, M. (2003). Modul geometri. Universitas Terbuka: Jakarta.
Siagian, M. D. (2016). Kemampuan koneksi matematik dalam pembelajaran matematika. Journal of Mathematics Education and Science, 2 (1), 58-67.
Su, H. F., Ricci, F. A., & Mnatsakanian, M. (2016). Mathematical teaching strategies: pathways to critical thinking and metacognition. Journal of Research in Education and Science (IJRES), 2 (1), 190-200.
Sun, Y., Li, S., Bonini, N., & Liu, Y. (2016). Effect of graph scale on risky choice: evidence from preference and process in decision-making. PLoS ONE, 11 (1), e0146914.
VanCleave, J. P. (1996). Gembira bermain dengan geometri: 101 percobaan yang pasti berhasil (Terjemahan: Pakar, D.). Pustaka Grafiti: Jakarta.
Zaslavsky, O., Sela, H., & Leron, U. (2002). Being sloppy about slope: the effect of changing the scale. Educational Studies in Mathematics, 49, 119-140.