Article Sidebar

Download
PDF
Statistic
Read Counter : 0 Download : 2

Main Article Content

Abstract

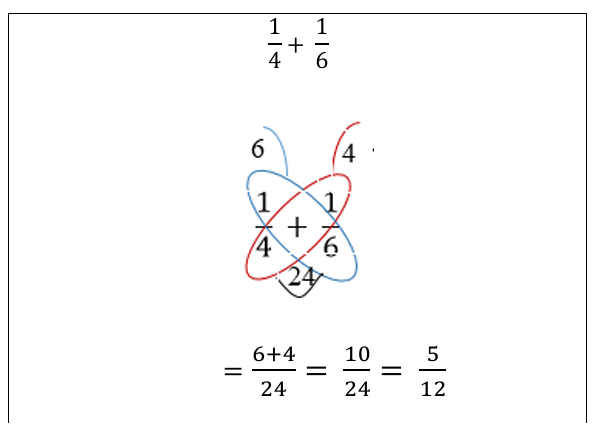
Several researches attempt to improve the performance in addition and subtraction of fraction by focusing on students’ understanding, such as applying fraction tiles manipulatives and number line in the teaching, or using visual aids such as area model and drawings or virtual diagrams. Similarly, few studies focus on adopting simple procedures that will facilitate students in attempting the topic. Butterfly Method is an approach that not only simplifies the pedagogical approach of learning addition and subtraction of fraction, but also indirectly promotes students’ conceptual understanding in the topic. Yet this approach is not commonly practiced in Brunei.  This action research employed quantitative approach involving fourty-one Year 9 IGCSE level students from a government secondary school in Brunei Darussalam. The study aimed to investigate the effect on applying Butterfly Method in the learning of addition and subtraction of fraction through pre-test and post-test.  The study revealed a significant improvement in students’ performance through Wilcoxon Signed rank test (Z = 4.2332, p-value < 0.05), with large effect size (r = 0.6611). This is also supported with the improvement of the overall mark distribution of students from pre-test to post-test, with Hake’s normalised gain values indicated majority of the participants achieved high (56.1%), medium (7.32%) and low (2.44%) improvements. Item analysis also indicated overall improvement of correct attempts in questions related to addition and subtraction of fraction, most apparently on fraction problems involving denominators not multiple of each other, improper fractions and mixed numbers. Thus, applying Butterfly Method significantly improved the overall students’ performance in the learning of addition and subtraction of fractions.


DOI: https://doi.org/10.22342/jpm.15.2.13934.161-174

Keywords

Addition and Subtraction of Fraction Butterfly Method

Article Details

License

Copyright (c) 2021 Dalilah Rauqah Laidin, Khairul Amilin Tengah

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.

All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).

How to Cite
Laidin, D. R., & Tengah, K. A. (2021). Applying Butterfly Method in the Learning of Addition and Subtraction of Fractions. Jurnal Pendidikan Matematika, 15(2), 161–174. Retrieved from https://jpm.ejournal.unsri.ac.id/index.php/jpm/article/view/235
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Bailey, D. H., Hoard, M. K., Nugent, L., & Geary, D. C. (2012). Competence with fractions predicts gains in mathematics achievement. Journal of Experimental Child Psychology, 113(3), 447-455. http://doi.org/10.1016/j.jecp.2012.06.004.
  2. Battista, C., Evans, T. M., Ngoon, T. J., Chen, T., Chen, L., Kochalka, J., & Menon, V. (2018). Mechanisms of interactive specialization and emergence of functional brain circuits supporting cognitive development in children. NPJ Science of Learning, 3(1), 1-11. https://doi.org/10.1038/s41539-017-0017-2.
  3. Beckmann. S. (2003). Mathematics for elementary teachers: Numbers and Operations (Vol. 1). Boston: Addison-Wesley.
  4. Boaler, J., Chen, L., Williams, C., & Cordero, M. (2016). Seeing as understanding: The importance of visual mathematics for our brain and learning. Journal of Applied & Computational Mathematics, 5(5), 1-6. https://doi.org/10.4172/2168-9679.1000325.
  5. Brousseau, G., Brousseau, N., & Warfield, V. (2004). Rationals and decimals as required in the school curriculum: Part 1: Rationals as measurements. The Journal of Mathematical Behavior, 23(1), 1–20. https://doi.org/10.1016/j.jmathb.2003.12.001.
  6. Bruce, C., Chang, D., Flynn, T., & Yearley, S. (2013). Foundations to learning and teaching fractions: Addition and subtraction. Retrieved from http://www.edugains.ca.
  7. Brown, J. D. (2002). The Cronbach alpha reliability estimate. JALT Testing & Evaluation SIG Newsletter, 6(1), 17-18.
  8. Castro, M. R., Custodio, A., & Escueta, M. G. (2013). Improving teacher instruction of addition of dissimilar fractions that integrated lesson study. Retrieved from http://www.academia.edu/.
  9. Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd Ed.). Hillsdale: Lawrence Erlbaum Associates.
  10. Coolican, H. (2017). Testing for differences between two samples. Research methods and statistics in psychology (6th ed., pp.438-486). London: Psychology Press.
  11. Damit D. H. S. P. H. (2002). Fraction concepts and skills of some Primary Six pupils in Brunei Darussalam. Unpublished Thesis. Gadong: Universiti Brunei Darussalam.
  12. Fazio, L., & Siegler, R. S. (2011). Teaching fractions. Brussels: International Academy of Education.
  13. Goswami, R. (2018). Misconceptions in fraction. At Right Anglesa, 7(1), 48-51.
  14. Hake, R. R. (1998) Interactive-engagement vs traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. American Journal of Physics, 66, 64-74. https://doi.org/10.1119/1.18809.
  15. Hansen, N., Jordan, N. C., & Rodrigues, J. (2017). Identifying learning difficulties with fractions: A longitudinal study of student growth from third through sixth grade. Contemporary Educational Psychology, 50, 45-59. https://doi.org/10.1016/j.cedpsych.2015.11.002.
  16. Harun, H., Z., H. (2003). The development of fractions and decimals concepts among Form 4 N-level students at a girls’ secondary school in Brunei Darussalam. Unpublished Thesis. Gadong: Universiti Brunei Darussalam.
  17. Huck, S. W., Cormier, W. H., & Bounds, W. G. (2012). Reading statistics and research (6th ed., Vol. 566, pp. 225-227). Boston: Pearson Education.
  18. Idris, N., & Narayanan, L. M. (2011). Error patterns in addition and subtraction of fractions among form two students. Journal of Mathematics Education, 4(2), 35-54.
  19. Khalid, M. (2007). Incorporating mathematical thinking in addition and subtraction of fraction: real issues and challenges. Progress report of the APEC-Khoen Kean international symposium: collaborative studies on innovations for teaching and learning mathematics in different cultures (II)-Lesson study focusing on mathematical thinking.
  20. Lortie-Forgues, H., Tian, J., & Siegler, R. S. (2015). Why is learning fraction and decimal arithmetic so difficult?. Developmental Review, 38, 201-221. http://doi.org/10.1016/j.dr.2015.07.008.
  21. Low, J., Shahrill, M. & Zakir, N. (2020). Solving fractions by applying the bar model concept with the butterfly method. Jurnal Pendidikan Matematika, 14(2), 101-116. https://doi.org/10.22342/jpm.14.2.11261.101-116.
  22. McCrory, R. (2006). Mathematicians and mathematics textbooks for prospective elementary teachers. Notices of the American Mathematical Society (AMS), 53(1), 20-29.
  23. Miller, G., & Obara, S. (2017). Finding meaning in mathematical mnemonics. Australian Mathematics Teacher, 73(3), 13-18.
  24. Ministry of Education. (2013). The national education system for the 21st century: SPN21. Berakas: Ministry of Education
  25. Orton, A., & Frobisher, L. (1996). Introduction to education: Insights into teaching mathematics (1st ed., Vol. 1). London: Cassell.
  26. Parker, T. H., & Baldridge, S. J. (2004). Elementary Mathematics for Teachers (Vol. 1). Okemos: Sefton-Ash Publishing.
  27. Rittle-Johnson, B., & Schneider, M. (2015). Developing conceptual and procedural knowledge of mathematics. Oxford Handbook of Numerical Cognition, 1118-1134.
  28. Rittle-Johnson, B., Siegler, R. S., & Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: An iterative process. Journal of Educational Psychology, 93(2), 346. http://doi.org/10.1037//0022-0663.93.2.346.
  29. Rockinson-Szapkiw, A. (2013). Statistics guide.Retrieved from http://amandaszapkiw.com/.
  30. Rosenthal, R. (1991). Meta-analytic procedures for social research. Thousand Oaks: Sage Publications.
  31. Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M. I., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691-697. http://doi.org/10.1177/0956797612440101
  32. Suffolk, J., & Clements, M. A. (2003). Fractions concepts and skills of form 1 and form 2 students in Brunei Darussalam. In H. S. Dhindsa, S. B. Lim, P. Achleitner, & M. A. Clements (Eds.), Studies in science, mathematics and technical education (pp. 145– 154). Universiti Brunei Darussalam.
  33. Tavakol, M., & Dennick, R. (2011). Making sense of Cronbach’s alpha. International Journal of Medical Education, 2, 53–55. https://dx.doi.org/10.5116%2Fijme.4dfb.8dfd.
  34. Yusof, J., & Malone, J. (Eds.). (2003). Mathematical errors in fractions: A case of Bruneian primary 5 pupils. Proceeding of the 26th annual conference of the mathematics education research group of Australasia. Mathematics Education Research Group of Australasia Incorporated.

Most read articles by the same author(s)

Similar Articles

1 2 3 4 5 > >> 

You may also start an advanced similarity search for this article.