Article Sidebar

Download
PDF
Statistic
Read Counter : 19 Download : 4

Main Article Content

Abstract

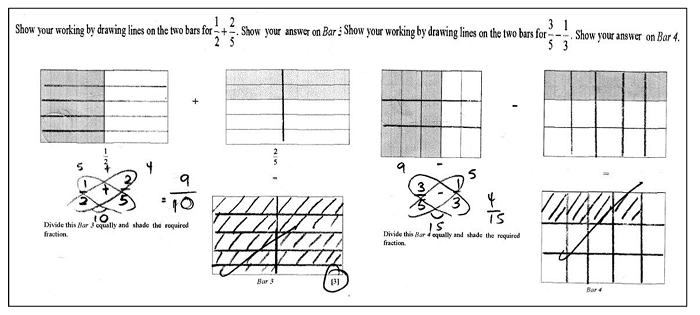
This study aims to investigate an intervention in the application of the Butterfly Method Algorithm with the Bar Model Concept on the addition and subtractions of Fractions to Year 9 students in one of the Government secondary schools in Brunei Darussalam. The Butterfly Method is an alternative visual method for teaching fractions where the diagonal and horizontal multiplication of the denominators and numerators are employed by drawing the Butterfly. A mixed-method approach was used to explore the impact of the intervention with data gathered from the students’ written pre- and post-tests and interview transcripts. The tests conducted before and after the intervention were used to analyze students’ errors and misconceptions. The students’ written analyses of the post-test results revealed that not all of the students applied the Butterfly Method. A few students were selected for interviews in order to gain deeper insights into how they developed the errors and misconceptions from both tests. Findings from the students’ interview transcripts revealed they were not confident with the Butterfly Method, and they needed more time to be familiar with the concept. Another factor for not applying the Butterfly Method is due to students’ confusion on subtracting fractions that has the same denominators as well as subtracting a proper fraction from a whole number. This study concluded that students who applied the Butterfly Method helped them to remember the new method from the intervention satisfactorily in comparison to those who lack the confidence in applying it.

Keywords

Fractions Butterfly Method Bar Model Concept Addition Subtraction

Article Details

License

Copyright (c) 2020 PDF

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.

All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).

How to Cite
Low, J., Shahrill, M., & Zakir, N. (2020). Solving Fractions by Applying the Bar Model Concept with the Butterfly Method. Jurnal Pendidikan Matematika, 14(2), 101–116. Retrieved from https://jpm.ejournal.unsri.ac.id/index.php/jpm/article/view/133
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Bruner, J. (1996). The culture of education. Cambridge, MA: Harvard University Press.
  2. Cardone, T. (2015). Nix the tricks: A guide to avoiding shortcuts that cut out math concept development (2nd Ed.). CreateSpace Independent Publishing Platform.
  3. Curriculum Development Department (2011). Framework and Guidelines for Curriculum and Assessment: Mathematics Year 7 and Year 8. Brunei Darussalam: Ministry of Education.
  4. Dhlamini, Z. B., & Kibirige, I. (2014). Grade 9 learners’ errors and misconceptions in addition of fractions. Mediterranean Journal of Social Sciences, 5(8), 236-244. http://dx.doi.org/10.5901/mjss.2014.v5n8p236.
  5. Duzenli-Gokalp, N., & Sharma, D. (2010). A study on addition and subtraction of fractions: The use of Pirie and Kieren model and hands-on activities. Procedia - Social and Behavioral Sciences, 2(2), 5168-5171. https://doi.org/10.1016/j.sbspro.2010.03.840.
  6. Emeny, W. (2014). Bar modelling - a powerful visual approach for introducing number topics. Retrieved from http://www.greatmathsteachingideas.com/2014/12/26/bar-modelling-a-powerful-visual-approach-for-introducing-number-topics/.
  7. Hunter, J., Hunter, R., & Restani, R. (2020). Exploring student views and perspectives within a changing classroom context: Developing mathematical enquiry communities with diverse learners. In A. MacDonald, L. Danaia, & S. Murphy (Eds.), STEM education across the learning continuum: early childhood to senior secondary (pp. 175-194). Singapore: Springer.
  8. Idris, N., & Narayanan, L. M. (2011). Error patterns in addition and subtraction of fractions among form two Students. Journal of Mathematics Education, 4(2), 35-54.
  9. Khalid, M., Saad, S., Hamid, S. R. A., Abdullah, M. R., Ibrahim, H., & Shahrill, M. (2020). Enhancing creativity and problem-solving skills through creative problem solving in teaching mathematics. Creativity Studies, 13(2), 270-291. https://doi.org/10.3846/cs.2020.11027.
  10. Madani, N. A., Tengah, K. A., & Prahmana, R. C. I. (2018, September). Using bar model to solve word problems on profit, loss and discount. Journal of Physics: Conference Series, 1097(1), 012103. https://doi.org/10.1088/1742-6596/1097/1/012103.
  11. Mattock, P. (2015). Adding and subtracting fractions with bar models – worth sticking with. Retrieved from http://educatingmrmattock.blogspot.com/2015/09/adding-and-subtracting-fractions-with.html.
  12. McLeod, S. A. (2008). Bruner-learning theory in education. Retrieved from http://www.simplypsychology.org/bruner.html
  13. Miller, G., & Obara, S. (2017). Finding meaning in mathematical mnemonics. The Australian Mathematics Teacher, 73(3), 13-18.
  14. Roslan, R., Panjang, M., Yusof, N., & Shahrill, M. (2018). Teacher’s feedback in teaching science in a bilingual Bruneian primary classroom. On the Horizon, 26(2), 122-136. https://doi.org/10.1108/OTH-09-2017-0080.
  15. Rosli, R., Han, S., Capraro, R., & Capraro, M. (2013). Exploring preservice teachers’ computational and representational knowledge of content and teaching fractions. Journal of Korean Society of Mathematics Education, 17(4), 221-241. https://doi.org/10.7468/jksmed.2013.17.4.221.
  16. Sarwadi, H. R. H., & Shahrill, M. (2014). Understanding students’ mathematical errors and misconceptions: The case of year 11 repeating students. Mathematics Education Trends and Research, 2014, 1–10. https://doi.org/10.5899/2014/metr-00051.
  17. Seah, R., & Booker, G. (2005). Lack of numeration and multiplication conceptual knowledge in middle school students: A barrier to the development of high school mathematics? In B. Bartlett, F. Bryer, & D. Roebuck (Eds.), Stimulating the ‘Action’ as participants in Participatory Research (Vol. 3, pp. 86-98). Nathan, QLD: Griffith University.
  18. Shahrill, M. (2013). Review of effective teacher questioning in mathematics classrooms. International Journal of Humanities and Social Science, 3(17), 224-231.
  19. Shahrill, M., & Clarke, D. J. (2014). Brunei teachers’ perspectives on questioning: Investigating the opportunities to ‘talk’ in mathematics lessons. International Education Studies, 7(7), 1-18. http://dx.doi.org/10.5539/ies.v7n7p1.
  20. Shahrill, M., & Mundia, L. (2014). The use of low-order and higher-order questions in mathematics teaching: Video analyses case study. Journal of Studies in Education, 4(2), 15-34. https://doi.org/10.5296/jse.v4i2.5318.
  21. Thirunavukkarasu, M., & Senthilnathan, S. (2014). Effectiveness of bar model in enhancing the learning of mathematics at primary level. International Journal of Teacher Educational Research, 3(1), 15-22.
  22. Wong, M., & Evans, D. (2007). Students’ conceptual understanding of equivalent fractions. In J. Watson & K. Beswick (Eds.), Mathematics: Essential research, essential practice. Proceedings of the 30th Annual Conference of the Mathematics Education Research Group of Australasia (Vol. 2, pp. 824-833). MERGA Inc.
  23. Yeap, B. H. (2010). Bar Modelling: A problem-solving tool. Singapore: Marshall Cavendish Education.
  24. Zakir, N. (2018). The impact of educational change processes in brunei preschools: An interpretive study. Unpublished Thesis. United Kingdom: University of Sheffield.

Most read articles by the same author(s)

Similar Articles

1 2 3 4 5 6 > >> 

You may also start an advanced similarity search for this article.