Article Sidebar

Download
PDF
Statistic
Read Counter : 25 Download : 1

Main Article Content

Abstract

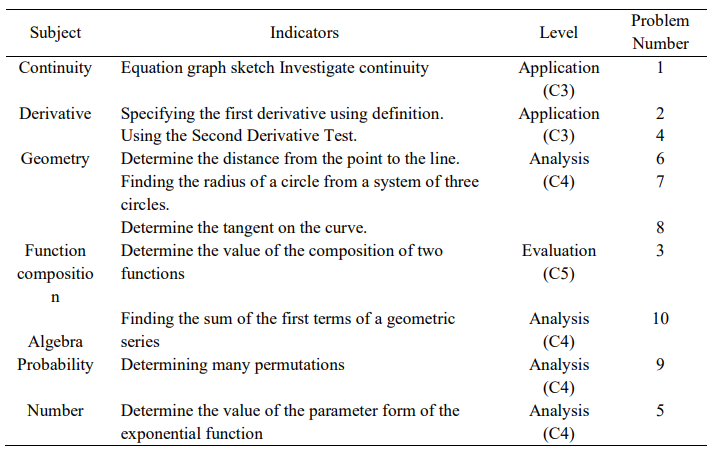
Instruments are tool that used to collect research data. The instrument consists of two types, namely the main and supporting instruments. In this paper, we develop the supporting instruments which are used in qualitative research such as commognitive perspective. The instrument development aims to explore and reveal students' cognition in understanding derivative tasks that are valid and reliable. It means the instrument is needed in order to explore cognition and communication in an inseparable manner according to the theory used in this research. The two supporting instruments that developed in this study are the mathematical ability test (MAT) and the derivatives understanding task (TMT). Moreover, the developed MAT instrument is accompanied by source questions, grids and indicators. The MAT consists of 10 questions, and this was tested empirically in the category of valid and high reliability. Furthermore, TMT is developed as a reference for exploring student commognition. The TMT consists of 14 questions. The preparation and development of the instruments in this study are based on relevant theories and supported by empirical data. At the expert review step, validation is carried out in terms of content, construct and language by experts. Each step is tested for readability, then suggestions and comments are provided for improvement. The final results obtained show that the two supporting instruments (MAT and TMT) are feasible to use in exploring student commognition because these bring up keywords, visual mediators, endorsed narratives, and routines, as a commognition character.


DOI: https://doi.org/10.22342/jpm.17.3.20826.343-360

Keywords

Commognition Development Instrument Derivative

Article Details

License

Copyright (c) 2023 Rita Lefrida, Tatag Yuli Eko Siswono, Agung Lukito

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.

All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).

How to Cite
Lefrida, R., Siswono, T. Y. E., & Lukito, A. (2024). Development of Derivative Understanding Task Instruments to Explore Student Commognition. Jurnal Pendidikan Matematika, 17(3), 343–360. Retrieved from https://jpm.ejournal.unsri.ac.id/index.php/jpm/article/view/156
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Adams, F. (2014). What is a Cognitive Process?. Found Sci, 19, 133–135. https://doi.org/10.1007/s10699-013-9324-0
  2. Anderson, W. L., & Krathwohl, D. R. (Ed.). (2001). A Taxonomy for Learning, Teaching, And Assessing: A Revision of Bloom’s Taxonomy of Educational Objectives. Addison Wesley Longman.
  3. Bell, H. F. (1978). Teaching and learning mathematics (in secondary school). Dubuque, lowa: Company Publishing.
  4. Bem, S. L. (1974). The measurement of psychological androgyny. Journal of Consulting and Clinical Psychology, 42(2), 155–162. https://doi.org/10.1037/h0036215
  5. Ben-Zvi, D., & Sfard, A. (2007). Ariadne’s thread, Daedalus’ wings’ and the learner’s autonomy. Education & Didactique, 1(3), 117–134. https://doi.org/10.4000/educationdidactique.241
  6. Berger, M. (2013). Examining mathematical discourse to understand in-service teachers’ mathematical activities. Pythagoras, 34(1), 1-10. http://dx.doi.org/10.4102/pythagoras.v34i1.197
  7. Brown, G., & Yule, G. (1983). Discourse Analysis. Cambridge University Press. https://doi.org/10.1017/CBO9780511805226
  8. Campbell, T., Abd-Hamid, N. H. & Chapman, H. (2010). Development of Instruments to Assess Teacher and Student Perceptions of Inquiry Experiences in Science Classrooms. J Sci Teacher Educ 21, 13–30. https://doi.org/10.1007/s10972-009-9151-x
  9. Creswell, J. W. (2014). Research design: Qualitative, quantitative, and mixed methods approaches. SAGE Publication.
  10. Dewi, S. S., Hariastuti, R. M., & Utami, A. U. (2019). Analysis of the level of difficulty and differentiating power of Mathematics Olympiad questions at junior high school level in 2018 [in Bahasa]. Transformasi: Jurnal Pendidikan Matematika Dan Matematika, 3(1), 15-26. https://doi.org/10.36526/tr.v3i1.388
  11. Ministry of Education. (2007). Big Indonesia Dictionary [in Bahasa]. Jakarta: Balai Pustaka.
  12. Ebel, R. L., & Frisbie, D. A. (1991) Essentials of Educational Measurement. 5th Edition, Prentice-Hall, Englewood Cliffs.
  13. Gallego-Sánchez, I., González, A., & Gavilán-Izquierdo, J. M. (2022). Analyzing pedagogical routines in the upper secondary school teacher’s discourse using the commognitive aproach. International Journal of Instruction, 15(3), 291-306. https://doi.org/10.29333/iji.2022.15316a
  14. Hiebert, J., & Carpenter, T.P. (1992). Learning and teaching with under- standing. In: D. A. Grouns (Ed.), Handbook of research on mathematics teaching and learning (pp. 65-92). New York: Macmillan.
  15. Hopkins, C. D., & Antes, R. L. (1999). Classroom Measurement and Evaluation. Illionis, F.E. Peacock
  16. Lavie, I., Steiner, A. & Sfard, A. (2019). Routines we live by: from ritual to exploration. Educ Stud Math, 101, 153–176. https://doi.org/10.1007/s10649-018-9817-4
  17. Kepner, M. D., & Neimark, E. D. (1984). Test-retes reability and differential patterns of score change on the Group Embedded Figures Test. Journal of Personality and Social Psychology. 46(6), 1405-1431. https://doi.org/10.1037/0022-3514.46.6.1405
  18. Ministry of Research, Technology and Higher Education. (2018). Question about Joint Selection to Enter State Universities (SBMPTN), TKD Science and Technology Field, Text Code 417 [in Bahasa].
  19. Lincoln, Y. S., & Guba, E. G. (1985). Naturalistic Inquiry. SAGE Publications
  20. Merriam, S. B. (1998). Qualitative research and case study applications in education. San Francisco : Jossey-Bass Publishers.
  21. Nardi, E., Ryve, A., Stadler, E., & Viirman, O. (2014). Commognitive analyses of the learning and teaching of mathematics at university level: The case of discursive shifts in the study of calculus. Research in Mathematics Education, 16(2), 182–198. https://doi.org/10.1080/14794802.2014.918338
  22. Park, J. (2013). Is the derivative a function? If so, how do students talk about it?. International Journal of Mathematical Education in Science and Technology, 44(5), 624–640. https://doi.org/10.1080/0020739X.2013.795248.
  23. Park, J. (2015). Erratum to: Is the derivative a function? If so, how do we teach it?. Educ Stud Math, 90, 231. https://doi.org/10.1007/s10649-015-9630-2
  24. Pourdavood, R. G., & Wachira, P. (2016). Importance of Mathematical Communication and Discourse in Secondary Classrooms. Global Journal of Science Frontier Research, 15.
  25. Ratumanan, T. G., & Laurens, T. (2011). Assessment of Learning Outcomes at the Education Unit Level (2nd Edition). Surabaya: Unesa University Press.
  26. Robbins, S. P., & Judge, T. A. (2007). Organizational behavior (12th ed.). Upper Saddle River, NJ: Pearson Prentice Hall.
  27. Robert, A., & Roux, K. (2018). A commognitive perspective on Grade 8 and Grade 9 learner thinking about linear equations. Pythagoras -Journal of the Association for Mathematics Education of South Africa, Pythagoras, 40(1), 438. https://doi.org/10.4102/pythagoras.v40i1.438
  28. Sfard, A., & Kieran, C. (2001). Cognition as communication: Rethinking learning-by-talking through multi-faceted analysis of students' mathematical interactions. Mind, Culture, and Activity, 8(1), 42–76. https://doi.org/10.1207/S15327884MCA0801_04
  29. Sfard, A. (2007). When the rules of discourse change, but nobody tells you: Making sense of mathematics learning from a commognitive standpoint. Journal of the Learning Science, 16(4), 567–615. http://dx.doi.org/10.1080/10508400701525253
  30. Sfard, A. (2008). Thinking as communicating: Human development, development of discourses, and mathematizing. Cambridge University Press.
  31. Sfard, A. (2012). Introduction: Developing mathematical discourse—Some insights from communicational research. Editorial / International Journal of Educational Research, 51–52, 1–9. https://doi.org/10.1016/j.ijer.2011.12.013
  32. Sfard, A. (2017). Ritual for Ritual, Exploration for Exploration or what Learners are Fffered is What They Present Back to you in Return. https://www.researchgate.net/publication/305066710
  33. Sfard, A. (2020). Commognition. In Stephen Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 91-101). International Publishing Springer Nature.
  34. Sugiyono. (2010). Metode Penelitian Pendekatan Kuantitatif, Kualitatif, R & D. Bandung: Penerbit Alfabeta.
  35. Tabach, M., & Nachlieli, T. (2016). Communicational perspectives on learning and teaching mathematics: Prologue. Educational Studies in Mathematics, 91(3), 299–306. https://doi.org/10.1007/s10649-015-9638-7
  36. Taber, K. T. (2018). The Use of Cronbach’s Alpha When Developing and Reporting Research Instruments in Science Education. Research in Science Education, 48, 1273-1296. https://doi.org/10.1007/s11165-016-9602-2
  37. Taib, F., & Yusoff, M. S. B. (2014). Difficulty index, discrimination index, sensitivity and specificity of long case and multiple choice questions to predict medical students’ examination performance. Journal of Taibah University Medical Sciences, 9(2), 110-114. https://doi.org/10.1016/j.jtumed.2013.12.002
  38. Thomas, G. T. (2009). Interpreting diagnostic test. Retrieved from http://gim.unmc. edu/dxtests/Default.htm.
  39. Varberg, D., Purcell, E. J., & Ridgon, S. (2010). Calculus (I. Nyoman, Trans.). Prentice Hall, Inc. (Original work published 2007)
  40. Wichelt, L. (2009). Communication: A Vital Skill of Mathematics. Retrieved from http://digitalcommons.unl.edu/mathmidactionresearch/18
  41. Wille, A. M. (2020). Activity with Signs and Speaking About It: Exploring Students’ Mathematical Lines of Thought Regarding the Derivative. International Journal of Science and Mathematics Education, 18, 1587–1611. https://doi.org/10.1007/s10763-019-10024-1
  42. Witkin, H. A., Oltman, P., Raskin, E., & Karp, S. (1971). A manual for the embedded figures test. Consulting Psychologists Press.
  43. Zayyadi, M., Subanji, Hidayanto, H., & Sulandra, I. M. (2019). A Commognitive Framework: The Process of Solving Mathematics Problems of Middle School Students. International Journal of Learning, Teaching and Educational Research, 18(2), 89-102. https://doi.org/10.26803/ijlter.18.2.7