Article Sidebar

article 08
Download
PDF
Statistic
Read Counter : 23 Download : 6

Main Article Content

Abstract

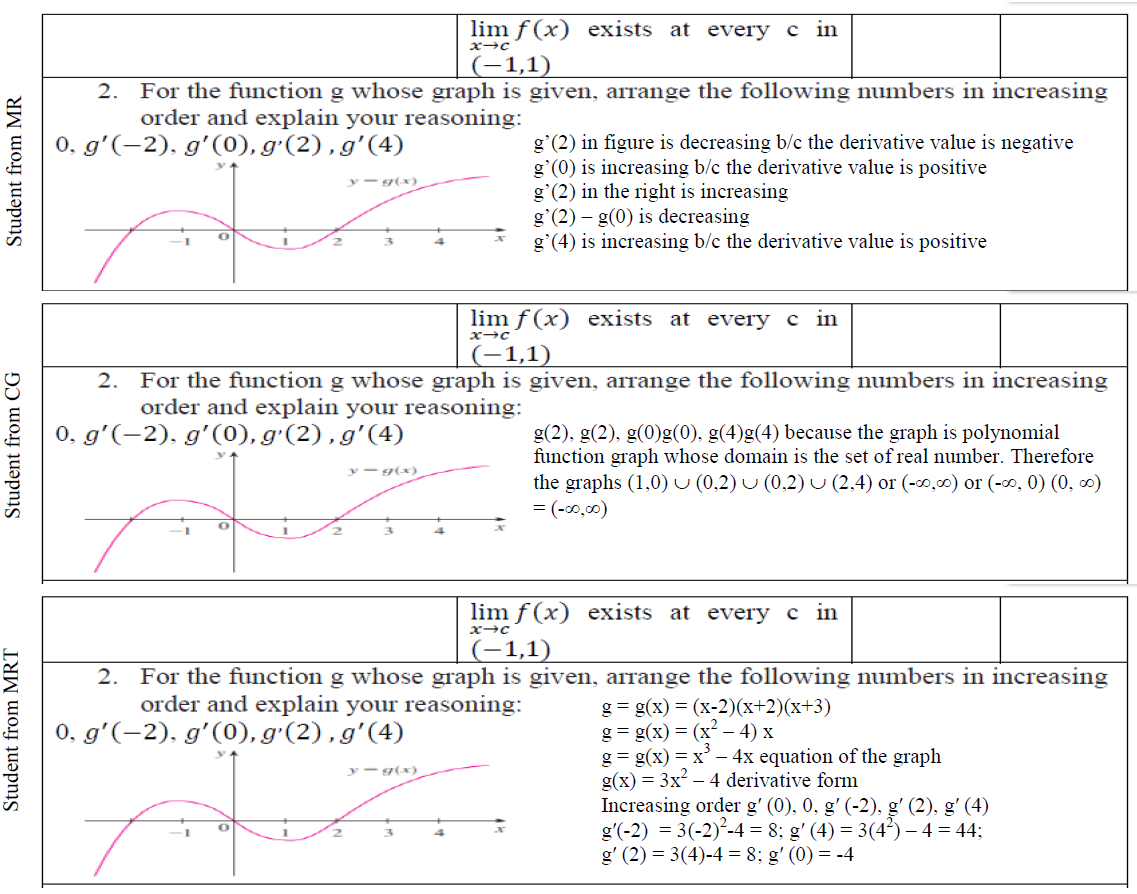
This study investigated the effect of the multiple representations approaches on students’ representation interpretation in learning calculus. Pretest and posttest quasi-experimental design of non-equivalent groups was used. Three intact groups of size 53, 57, and 54 students from Jigjiga and Kebri-Dehar Universities in Ethiopia participated in this study. The groups included a GeoGebra-supported multiple representations approach (MRT) from Jigjiga University, a multiple representation approach (MR), and a conventional approach (CG), both from Kebri Dehar University. Representation interpretation problem pretest and posttest were administered compiled from pre and calculus contents, respectively. Students’ performance on representation interpretation problems was assessed using rubric scores, and their interpretation techniques were labeled as local versus global and syntactic versus semantic. Results revealed no statistically significant mean difference among the three groups on representation interpretation from the posttest that was determined by one-way ANOVA ((F(2.161) = 2.232, P = .111 , Partial eta = .03). More students in each group demonstrated local and semantic interpretation than global and syntactic interpretation. After the treatment, many students from each group shifted towards the local and semantic interpretation. It is recommended that the study need to replicate other calculus contents with different participants to generalize the results of the study.

DOI:  https://doi.org/10.22342/jpm.16.3.18291.351-372

Keywords

GeoGebra Multiple Representations Representation Interpretations Calculus

Article Details

License

Copyright (c) 2022 Niguse Arefaine, Kassa Michael, Shimelis Assefa

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.

All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).

How to Cite
Arefaine, N., Michael, K., & Assefa, S. (2024). Effect of Multiple Representations on Students’ Performance on Interpretations and Techniques of Representation in Calculus. Jurnal Pendidikan Matematika, 16(3), 351–372. Retrieved from https://jpm.ejournal.unsri.ac.id/index.php/jpm/article/view/154
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Adu-Gyamfi, K., Stiff, L., & Bossé, M. J. (2012). Lost in translation: Examining translation errors associated with mathematical representations. School Science and Mathematics, 112(3), 159- 170. https://doi.org/10.1007/s10763-016-9730-1.
  2. Adu-Gyamfi, K., Bossé, M. J., & Chandler, K. (2017). Student connections between algebraic and graphical polynomial representations in the context of a polynomial relation. International Journal of Science and Mathematics Education, 15(5), 915-938, https://doi.org/10.1007/s10763-016-9730-1.
  3. Adu-Gyamfi, K., Bossé, M. J., & Lynch‐ Davis, K. (2019). Three types of mathematical representational translations: Comparing empirical and theoretical results. School Science and Mathematics, 119(7), 396-404, https://doi.org/10.1111/ssm.12360.
  4. Ainsworth, S. (1999). The functions of multiple representations. Computers & Education, 33(2-3), 131-152, https://doi.org/10.1016/S0360-1315(99)00029-9.
  5. Ainsworth, S. (2008). The educational value of multiple-representations when learning complex scientific concepts. Visualization: Theory and Practice in Science Education (pp. 191-208): Springer, https://doi.org/10.1007/978-1-4020-5267-5_9.
  6. Andersen, C., Scheuer, N., Echeverría, M. d. P. P., & Teubal, E. (2009). Representational systems and practices as learning tools: Sense Publishers Rotterdam. https://doi.org/10.1163/9789087905286
  7. Bennett, A., Moore, T., & Nguyen, X. (2011). A longitudinal study on students' development and transfer of the concept of integration. Paper presented at the Conference & Exposition, American Society for Engineering Education, Vancouver, British Columbia, Canada. https://doi.org/10.18260/1-2--17338
  8. Berry, K. J., & Mielke Jr, P. W. (1988). A generalization of Cohen's kappa agreement measure to interval measurement and multiple raters. Educational and Psychological Measurement, 48(4), 921-933.
  9. Bossé, M. J., Adu-Gyamfi, K., & Chandler, K. (2014). Students' Differentiated Translation Processes. International Journal for Mathematics Teaching & Learning, Retrieved from http://www.cimt.org.uk/journal/bosse5.pdf.
  10. Chang, B. L., Cromley, J. G., & Tran, N. (2016). Coordinating multiple representations in a reform calculus textbook. International Journal of Science and Mathematics Education, 14(8), 1475- 1497. https://doi.org/10.1007/s10763-015-9652-3.
  11. Demetriadis, S. (2004). Interaction between learner's internal and external representations in multimedia environment: a state-of-the-art.
  12. Dreyfus, T., & Eisenberg, T. (1996). Mathematical Thinking. The nature of mathematical thinking, 253-284.
  13. Dunham, P. H., & Osborne, A. (1991). Learning How to See: Students Graphing Difficulties. Focus on learning problems in mathematics, 13(4), 35-49.
  14. Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1-2), 103-131, http://dx.doi.org/10.1007/s10649-006- 0400-z.
  15. Easdown, D. (2009). Syntactic and semantic reasoning in mathematics teaching and learning. International Journal of Mathematical Education in Science and Technology, 40(7), 941-949, https://doi.org/10.1080/00207390903205488.
  16. Ernaningsih, Z., & Wicasari, B. (2017). Analysis of Mathematical Representation, Communication, and Connection in Trigonometry. Paper presented at the the 2017 International Conference on Research in Education.
  17. Gagatsis, A., & Elia, I. (2004). The Effects of Different Modes of Representation on Mathematical Problem Solving. International Group for the Psychology of Mathematics Education, URL: https://gnosis.library.ucy.ac.cy/handle/7/38008.
  18. Gagatsis, A., & Shiakalli, M. (2004). Ability to translate from one representation of the concept of function to another and mathematical problem solving. Educational Psychology, 24(5), 645- 657, https://doi.org/10.1080/0144341042000262953.
  19. Gemechu, E., Kassa, M., & Atnafu, M. (2018). MATLAB Supported Learning and Students' Conceptual Understanding of Functions of Two Variables: Experiences from Wolkite University. Bulgarian Journal of Science and Education Policy, 12(2), 314-344.
  20. Grossberg, S. (1982). How does a brain build a cognitive code? Studies of Mind and Brain (pp. 1-52): Springer.
  21. Haciomeroglu, E. S., & Andreasen, J. B. (2013). Exploring calculus with dynamic mathematics software. Mathematics and Computer Education, 47(1), 6.
  22. Huang, C. H. (2015). Calculus students’ visual thinking of definite integral. American Journal of Educational Research, 3(4), 476-482.
  23. Huntley, M. A., Marcus, R., Kahan, J., & Miller, J. L. (2007). Investigating high-school students’ reasoning strategies when they solve linear equations. The Journal of Mathematical Behavior, 26(2), 115-139, doi:10.1016/j.jmathb.2007.05.005.
  24. Inzunza, S. (2006). Student’s errors and difficulties for solving problems of sampling distributions by means of computer simulation. ICOTS-7, 1–4.
  25. Kaput, J. (1989). Linking representations in the symbol systems of algebra', Wagner, S. & Kieran, C.(Eds.), Research Issues in the Learning and Teaching of Algebra: Lawrence Erlbaum, Hillsdale, NJ.
  26. Leinhardt, G., Zaslavsky, O., & Stein, M. K. (1990). Functions, graphs, and graphing: Tasks, learning, and teaching. Review of Educational Research, 60(1), 1-64, URL: https://doi.org/10.3102/00346543060001001.
  27. National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. Reston VA: NCTM.
  28. National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all. Reston VA: NCTM.
  29. Nguyen, D. H., & Rebello, N. S. (2009). Students’ difficulties in transfer of problem solving across representations. Paper presented at the AIP Conference Proceedings.
  30. Niemi, D. (1996). Assessing conceptual understanding in mathematics: Representations, problem solutions, justifications, and explanations. The Journal of Educational Research, 89(6), 351- 363, https://doi.org/10.1080/00220671.1996.9941339.
  31. Palmer, S.E. (1978). Fundamental aspects of cognitive representation. In Eleanor Rosch & Barbara Lloyd (eds.), Cognition and Categorization. Lawrence Elbaum Associates. pp. 259-303 (1978).
  32. Pambudi, D. S., Budayasa, I. K., & Lukito, A. (2020). The role of mathematical connections in mathematical problem solving. Jurnal Pendidikan Matematika, 14(2), 129-144, https://doi.org/10.22342/jpm.14.2.10985.129-144.
  33. Panasuk, R., & Beyranevand, M. (2011). Middle school algebra students’ preferred representations when solving problems. The Mathematics Educator, 13(1), 32-52.
  34. Rachma, A. A., & Rosjanuardi, R. (2021). Students’ obstacles in learning sequence and series using onto-semiotic approach. Jurnal Pendidikan Matematika, 15(2), 115-132, https://doi.org/10.22342/jpm.15.2.13519.115-132
  35. Rahmawati, D. (2019). Translation Between Mathematical Representation: How Students Unpack Source Representation? Matematika dan Pembelajaran, 7(1), 50-64, https://doi.org/10.33477/mp.v7i1.1045.
  36. Rahmawati, D., Purwantoa, S., Hidayanto, E., & Anwar, R. B. (2017). Process of Mathematical Representation Translation from Verbal into Graphic. International Electronic Journal of Mathematics Education, https://doi.org/10.29333/iejme/618.
  37. Roth, W.-M., & Bowen, G. M. (2001). Professionals read graphs: A semiotic analysis. Journal for Research in Mathematics Education, 159-194, https://doi.org/10.2307/749672.
  38. Salkind, G. M., & Hjalmarson, M. (2007). Mathematical representations. http://mason.gmu. edu/~ gsalkind/portfolio/products/857LitReview.pdf. Di akses tanggal, 15.
  39. Teferra, T., Asgedom, A., Oumer, J., & Assefa, B. (2017). Ethiopian Education Development Roadmap (2017-30), Retrieved from: https://moe.gov.et.
  40. Van Labeke, Nicolas and Ainsworth, Shaaron E. (2001). Applying the DeFT Framework to the Design of Multi-Representational Instructional Simulations. In: AIED’01 - 10th International Conference on Artificial Intelligence in Education, 19-23 May 2001, San Antonio, Texas, IOS Press, pp. 314–321.
  41. Widodo, S.A., Pangesti, A.D., Istiqomah, I., Kuncoro, K.S., & Arigiyati, T.A. (2020). Thinking process of concrete student in solving two-dimensional problems. Jurnal Pendidikan Matematika, 14(2), 117-128, https://doi.org/10.22342/jpm.14.2.9460.117-128.
  42. Yusuf, M., Rahim, S. S. A., & Eu, L. K. (2021). Obstacles faced by college students in solving probability word problems. Jurnal Pendidikan Matematika, 15(1), 83-90, https://doi.org/10.22342/jpm.15.1.12801.83-90.