Analysis of Concept Construction and Student Errors on the Topic of Double Integral Based on APOS Theory

Yarman Yarman; Yerizon Yerizon; Fitrani Dwina; Dewi Murni; Kelly Angelly Hevardani

doi:10.22342/jpm.v18i3.pp367-386

Download

PDF

Statistic

Read Counter : 227 Download : 83

Abstract

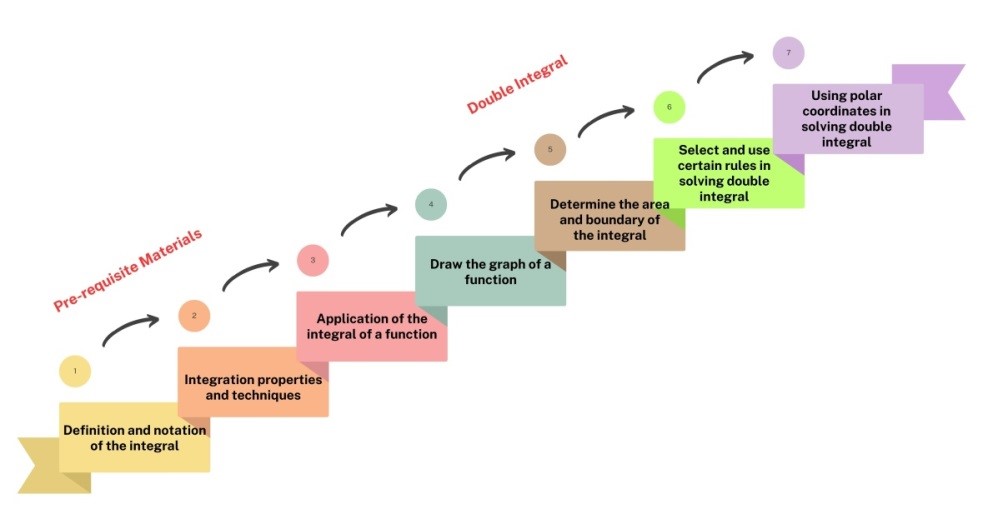
Integral learning is particularly challenging for students, primarily due to misconceptions predominantly caused by students' lack of understanding about functions, limits, and derivatives. Therefore, this research aims to investigate students’ thinking processes when solving double integral using Action, Process, Object, and Schema (APOS) theory, with a focus on past errors. In order to achieve the objective, a descriptive qualitative method was adopted. Data was collected from tests, interviews, and relevant documentation, and tested for validity using triangulation methods. The obtained results showed that high-ability students understood APOS stages in solving double integral. However, at the object stage, a lack of thoroughness in simplifying algebra led to misunderstandings. Medium-Ability Student (MS) was observed to successfully reach APOS stages when solving double integral using polar coordinates. Low-Ability Student (LS), on the other hand, showed inadequate understanding at the process stage, as evidenced by the failure to correctly draw the area and set integral boundaries. During the course of this investigation, process errors were found to be commonly associated with the calculations of double integral. In order to address these issues, Genetic Decomposition (GD) should be designed for other calculus topics, and error classification expanded to enhance the effectiveness of lectures.

Keywords

APOS Theory Double Integral Erros Genetic Decomposition

License

This work is licensed under a Creative Commons Attribution 4.0 International License.

This journal provides immediate open access to its content on the principle that making research freely available to the public supports a greater global exchange of knowledge.

All articles published Open Access will be immediately and permanently free for everyone to read and download. We are continuously working with our author communities to select the best choice of license options, Creative Commons Attribution-ShareAlike (CC BY-NC-SA).

How to Cite

Yarman, Y., Yerizon, Y., Dwina, F., Murni, D., & Hevardani, K. A. (2024). Analysis of Concept Construction and Student Errors on the Topic of Double Integral Based on APOS Theory. Jurnal Pendidikan Matematika, 18(3), 367–386. https://doi.org/10.22342/jpm.v18i3.pp367-386

Download Citation

References

Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education. New York: Springer. http://dx.doi.org/10.1007/978-1-4614-7966-6
Artigue, M. (1991). Analysis in Advanced Mathematical Thinking.
Avgerinos, E., & Remoundou, D. (2021). The Language of Rate of Change in Mathematics. European Journal of Investigation in Health, Psychology and Education, 11, 1599–1609. https://doi.org/10.3390/ejihpe11040113
Bangaru, S. P., Michel, J., Mu, K., Bernstein, G., Li, T. M., & Ragan-Kelley, J. (2021). Systematically Differentiating Parametric Discontinuities. ACM Transactions on Graphics, 40(4), 1–18. https://doi.org/10.1145/3450626.3459775
Bansilal, S., & Mkhwanazi, T. W. (2021). Pre-service Student Teachers’ Conceptions of the Notion of Limit. International Journal of Mathematical Education in Science and Technology, 1–19. https://doi.org/10.1080/0020739X.2020.1864488
Bansilal, S., Brijlall, D., & Trigueros, M. (2017). An APOS Study on Pre-service Teachers’ Understanding of Injections and Surjections. Journal of Mathematical Behavior, 48, 22–37. https://doi.org/10.1016/j.jmathb.2017.08.002
Baye, M. G., Ayele, M. A., & Wondimuneh, T. E. (2021). Implementing GeoGebra Integrated with Multi-teaching Approaches Guided by the APOS Theory to Enhance Students’ Conceptual Understanding of Limit in Ethiopian Universities. Heliyon, 7, 1–13. https://doi.org/10.1016/j.heliyon.2021.e07012
Bikner-Ahsbahs, A., & Prediger, S. (2014). Networking of Theories as a Research Practice in Mathematics Education. Switzerland: Springer. https://doi.org/10.1007/978-3-319-05389-9
Borji, V., & Font, V. (2019). Exploring Students’ Understanding of Integration by Parts: A Combined Use of APOS and OSA. EURASIA: Journal of Mathematics, Science and Technology Education, 15(7), 1–13. https://doi.org/10.29333/ejmste/106166
Borji, V., & Martínez-Planell, R. (2023). On Students’ Understanding of Volumes of Solids of Revolution: An APOS Analysis. Journal of Mathematical Behavior, 70, 1–20. https://doi.org/10.1016/j.jmathb.2022.101027
Borji, V., Alamolhodaei, H., & Radmehr, F. (2018). Application of the APOS-ACE Theory to Improve Students’ Graphical Understanding of Derivative. EURASIA Journal of Mathematics, Science and Technology Education, 14(7), 2947–2967. https://doi.org/10.29333/ejmste/91451
Bressoud, D. M. (2021). The Strange Role of Calculus in the United States. ZDM–Mathematics Education, 53(3), 521–533. https://doi.org/10.1007/s11858-020-01188-0
Bressoud, D., Burn, H., Hsu, E., Mesa, W., Rasmussen, C., & White, N. (2014). Successful Calculus Programs: Two-year Colleges to Research Universities. USA: NCTM.
Brijlall, D., & Ndlazi, N. J. (2019). Analyzing Engineering Students’ Understanding of Integration to Propose a Genetic Decomposition. Journal of Mathematical Behavior, 55, 1–12. https://doi.org/10.1016/j.jmathb.2019.01.006
Burgos, M., Bueno, S., Godino, J. D., & Pérez, O. (2021). Onto-semiotic Complexity of the Definite Integral: Implications for Teaching and Learning Calculus. REDIMAT – Journal of Research in Mathematics Education, 10(1), 4–40. https://doi.org/10.17583/redimat.2021.6778
Chapell, K. K., & Kilpartrick, K. (2003). Effects of Concept-based Instruction on Students’ Conceptual Understanding and Procedural Knowledge of Calculus. PRIMUS, 13(1), 17–37. https://doi.org/10.1080/10511970308984043
Cline, K., Parker, M., Zullo, H., & Stewart, A. (2013). Addressing Common Student Errors with Classroom Voting in Multivariable Calculus. PRIMUS, 23(1), 60–75. https://doi.org/10.1080/10511970.2012.697098
Díaz-Berrios, T., & Martínez-Planell, R. (2022). High School Student Understanding of Exponential and Logarithmic Functions. Journal of Mathematical Behavior, 66, 1–20. https://doi.org/10.1016/j.jmathb.2022.100953
Dominguez, A., Barniol, P., & Zavala, G. (2017). Test of Understanding Graphs in Calculus: Test of Students’ Interpretation of Calculus Graphs. EURASIA Journal of Mathematics, Science and Technology Education, 13(10), 6507–6531. https://doi.org/10.12973/ejmste/78085
Dubinsky, E. (2013). Using a Theory of Learning in College Mathematics Courses. MSOR Connections, 1(2), 10–15.
Ergene, Ö. & Özdemir, A. Ş. (2020). Investigating Pre-service Elementary Mathematics Teachers’ Perception of Integral. Journal of Educational Sciences, 51(51), 155–176. https://doi.org/10.15285/maruaebd.622149
Ergene, Ö. (2014). Investigation of Personal Relationship in Integral Volume Problems Solving Process within Communities of Practices. Dissertation. Marmara University.
Ergene, Ö., & Özdemir, A. Ş. (2022). Understanding the Definite Integral with the Help of Riemann Sums. Participatory Educational Research, 9(3), 445–465. https://doi.org/10.17275/per.22.75.9.3
Fernandez, A., & Mohammed, P. (2021). Hermite‐Hadamard Inequalities in Fractional Calculus Defined Using Mittag‐Leffler Kernels. Mathematical Methods in the Applied Sciences, 44(10), 8414–8431. https://doi.org/10.1002/mma.6188
Ferrini-Mundi, J., & Graham, K. (1994). Research in Calculus Learning: Understanding of Limits, Derivatives and Integrals. In J. J. Kaput & E. Dubinsky (eds.), Research Issues in Undergraduate Mathematics Learning, (pp.31–45). Washington DC: MAA.
Figueroa, A. P., Possani, E., & Trigueros, M. (2017). Matrix Multiplication and Transformations: An APOS Approach. Journal of Mathematical Behavior, 1–15. https://doi.org/10.1016/j.jmathb.2017.11.002
Font, V., Trigueros, M., Badillo, E., & Rubio, N. (2016). Mathematical Objects through the Lens of Two Different Theoretical Perspectives: APOS and OSA. Educational Studies in Mathematics, 91(1), 107–122. https://doi.org/10.1007/s10649-015-9639-6
Frank, K., & Thompson, P. W. (2021). School Students’ Preparation for Calculus in the United States. ZDM–Mathematics Education, 53(3), 549–562. https://doi.org/10.1007/s11858-021-01231-8
García-Martínez, I., & Parraguez, M. (2017). The Basis Step in the Construction of the Principle of Mathematical Induction Based on APOS Theory. Journal of Mathematical Behavior, 46, 128–143. https://doi.org/10.1016/j.jmathb.2017.04.001
Harel, G. (2017). The Learning and Teaching of Linear Algebra: Observations and Generalizations. The Journal of Mathematical Behavior, 46, 69–95. https://doi.org/10.1016/j.jmathb.2017.02.007
Hong, D. S., Choi, K. M., Hwang, J., & Runnalls, C. (2017). Integral Students’ Experiences: Measuring Instructional Quality and Instructors’ Challenges in Calculus 1 Lessons. International Journal of Research in Education and Science, 3(2), 424–437. https://doi.org/10.21890/ijres.327901
Kiat, S. E. (2005). Analysis of Students’ Difficulties in Solving Integration Problems. The Mathematics Educator, 9(1), 39–59.
Lam, T. T., Guan, T. E., & Luen, T. C. (2021). Fallacies About the Derivative of the Trigonometric Sine Function. The Mathematician Educator, 2(1), 1–10.
Li, V. L., Julaihi, N. H., & Eng, T. H. (2017). Misconceptions and Errors in Learning Integral Calculus. Asian Journal of University Education, 13(1), 17–39. https://ir.uitm.edu.my/id/eprint/21914
Maharaj, A. (2014). An APOS Analysis of Natural Science Students’ Understanding of Integration. REDIMAT – Journal of Research in Mathematics Education, 3(1), 54–73. https://doi.org/10.4471/redimat.2014.40
Mahir N. (2009). Conceptual and Procedural Performance of Undergraduate Students in Integration. International Journal of Mathematical Education in Science and Technology, 40(2), 201–211. https://doi.org/10.1080/00207390802213591
Marsitin, R. (2017). Koneksi Matematis dan Berpikir Kreatif dalam Pembelajaran Matematika dengan Teori APOS [Mathematical Connection and Creative Thinking in Mathematics Learning with APOS Theory]. Al-Khwarizmi: Jurnal Pendidikan Matematika dan Ilmu Pengetahuan Alam, 5(1), 87–100. https://doi.org/10.24256/jpmipa.v5i1.268
Martínez-Planell, R., & Trigueros, M. (2019). Using Cycles of Research in APOS: The Case of Functions of Two Variables. Journal of Mathematical Behavior, 55, 1–22. https://doi.org/10.1016/j.jmathb.2019.01.003
Martínez-Planell, R., & Trigueros, M. (2020). Students’ Understanding of Riemann Sums for Integrals of Functions of Two Variables. Journal of Mathematical Behavior, 59, 1–26. https://doi.org/10.1016/j.jmathb.2020.100791
Martínez-Planell, R., & Trigueros, M. (2021). Multivariable Calculus Results in Different Countries. ZDM – Mathematics Education, 53, 695–707. https://doi.org/10.1007/s11858-021-01233-6
Martínez-Planell, R., Trigueros, M., & Borji, V. (2022). The Relation Between Riemann Sums and Double Integrals: Results of a Second Research Cycle. Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education, 3, 179–186. http://hdl.handle.net/10045/126627
Mateus, E. (2016). Teaching Analysis to Process Integration Method Instruction by Parties. Bolema: Boletim de Educação Matemática, 30(55), 559–585. https://doi.org/10.1590/1980-4415v30n55a13
McGee, D., & Martínez-Planell, R. (2014). A Study of Semiotic Registers in the Development of the Definite Integral of Functions of Two and Three Variables. International Journal of Science and Mathematics Education, 12(4), 883–916. https://doi.org/10.1007/s10763-013-9437-5
Metaxas, N. (2007). Difficulties on Understanding the Indefinite Integral. In Woo, J. H., Lew, H. C., Park, K. S., Seo, D. Y. (Eds.). Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, 3, 265–272.
Miller, R. L., Santana-Vega, E., & Terrell, M. S. (2006). Can Good Questions and Peer Discussion Improve Calculus Instruction? PRIMUS, 16(3), 193–203. https://doi.org/10.1080/10511970608984146
Misu, L., Budayasa, I. K., Lukito, A., Hasnawati., & Rahim, U. (2019). Profile of Metacognition of Mathematics Education Students in Understanding the Concept of Integral in Category Classifying and Summarizing. International Journal of Instruction, 12(3), 481–496. https://doi.org/10.29333/iji.2019.12329a
Nagle, C., Martínez-Planell, R., & Moore-Russo, D. (2019). Using APOS Theory as a Framework for Considering Slope Understanding. Journal of Mathematical Behavior, 54, 1–14. https://doi.org/10.1016/j.jmathb.2018.12.003
Newman, M. A. (1977). An Analysis of Sixth-grade Pupils’ Error on Written Mathematical Tasks. Victorian Institute for Educational Research Bulletin, 39, 31–43. https://cir.nii.ac.jp/crid/1573105976160816128
Oktaç, A., Trigueros, M., & Romo, A. (2019). APOS Theory: Connecting Research and Teaching. For the Learning of Mathematics, 39(1), 33–37. https://www.jstor.org/stable/26742010
Orton, A. (1983). Students’ Understanding of Integration. Educational Studies in Mathematics, 14(1), 1–18. https://doi.org/10.1007/BF00704699
Pepper, R., Stephanie, V. C., Steven J. P., & Katherine K. P. (2012). Observations on Student Difficulties with Mathematics in Upper-division Electricity and Magnetism. Physical Review Special Topics – Physics Education Research, 8(1), 1–15. https://doi.org/10.1103/PhysRevSTPER.8.010111
Perfekt, K. M. (2021). Plasmonic Eigenvalue Problem for Corners: Limiting Absorption Principle and Absolute Continuity in the Essential Spectrum. Journal de Mathématiques Pures et Appliquées, 145, 130–162. https://doi.org/10.1016/j.matpur.2020.07.001
Rasslan, S., & Tall, D. (2002). Definitions and Images for the Definite Integral Concept. Proceedings of the 26th PME, 4, 89–96.
Seah, E. K. (2005). Analysis of Students’ Difficulties in Solving Integration Problems. The Mathematics Educator, 9(1), 39–59.
Sealey, V. (2008). Calculus Students’ Assimilation of the Riemann Integral into a Previously Established Limit Structure. Dissertation. Arizona State University.
Şefik, Ö., & Dost, Ş. (2020). The Analysis of the Understanding of the Three-dimensional (Euclidian) Space and the Two-variable Function Concept by University Students. Journal of Mathematical Behavior, 57, 1–19. https://doi.org/10.1016/j.jmathb.2019.03.004
Sholihah, U., & Maryono. (2020). Students’ Visual Thinking Ability in Solving the Integral Problem. Journal of Research and Advances in Mathematics Education, 5(2), 175–186. https://doi.org/10.23917/jramathedu.v5i2.10286
Siyepu, S. W. (2015). Analysis of Errors in Derivatives of Trigonometric Functions. International Journal of STEM Education, 2(16), 1–16. https://doi.org/10.1186/s40594-015-0029-5
Sofronas, K. S. (2011). What does it Mean for a Student to Understand the First-year Calculus? Perspectives of 24 Experts. The Journal of Mathematical Behavior, 30(2), 131–148. https://doi.org/10.1016/j.jmathb.2011.02.001
Swan, M. (2001). Dealing with Misconceptions in Mathematics. In Gates, P. (Ed.), Issues in Mathematics Teaching, (pp. 147–165). London: Routledge Falmer.
Syamsuri., & Santosa, C. (2021). Thinking Structure of Students’ Understanding of Probability Concept in Term of APOS Theory. MaPan: Jurnal Matematika dan Pembelajaran, 9(1), 119–135. https://doi.org/10.24252/mapan.2021v9n1a8
Syarifuddin, A., & Sari, A. F. (2021). Misconceptions of Prospective Mathematics Teacher on Graphing Function. Journal of Physics: Conference Series, 1869(1), 1–6. https://doi.org/10.1088/1742-6596/1869/1/012115
Tall, D. (1985). Understanding the Calculus. Mathematics Teaching, 110, 49–53.
Tall, D. (2011). Looking for the Bigger Picture. For the Learning of Mathematics, 31(2), 17–18.
Tall, D. (2014). Making Sense of Mathematical Reasoning and Proof. In Fried, M., Dreyfus, T. (Ed)., Mathematics & Mathematics Education: Searching for Common Ground, (pp. 223–235). New York: Springer. https://doi.org/10.1007/978-94-007-7473-5_13
Talley, J. R. (2009). Calculus Instructors’ Responses to Prior Knowledge Errors. Dissertation. University of Oklahoma, United States.
White, P., & Mitchelmore, M. (1996). Conceptual Knowledge in Introductory Calculus. Journal for Research in Mathematics Education, 27(1), 79–95. https://doi.org/10.5951/jresematheduc.27.1.0079
Wibawa, K. A., Nusantara, T., Subanji., & Parta, I. N. (2017). Fragmentation of Thinking Structure’s Students to Solving the Problem of Application Definite Integral in Area. International Education Studies, 10(5), 48–60. https://doi.org/10.5539/ies.v10n5p48
Zullo, H., Cline, K., Parker, M., Buckmire, R., George, J., Gurski, K., Larsen, J., Mellor, B., Oberweiser, J., Peterson, D., Spindler, R., Stewart, A., & Storm, C. (2011). Student Surveys: What do They Think? Mathematical Association of America, 29–34. https://doi.org/10.1017/CBO9781614443018.006
Zwanch, K. (2019). A Preliminary Genetic Decomposition of Probabilistic Independence. The Mathematics Educator, 28(1), 3–26. https://files.eric.ed.gov/fulltext/EJ1225414.pdf

References

Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education. New York: Springer. http://dx.doi.org/10.1007/978-1-4614-7966-6

Artigue, M. (1991). Analysis in Advanced Mathematical Thinking.

Avgerinos, E., & Remoundou, D. (2021). The Language of Rate of Change in Mathematics. European Journal of Investigation in Health, Psychology and Education, 11, 1599–1609. https://doi.org/10.3390/ejihpe11040113

Bangaru, S. P., Michel, J., Mu, K., Bernstein, G., Li, T. M., & Ragan-Kelley, J. (2021). Systematically Differentiating Parametric Discontinuities. ACM Transactions on Graphics, 40(4), 1–18. https://doi.org/10.1145/3450626.3459775

Bansilal, S., & Mkhwanazi, T. W. (2021). Pre-service Student Teachers’ Conceptions of the Notion of Limit. International Journal of Mathematical Education in Science and Technology, 1–19. https://doi.org/10.1080/0020739X.2020.1864488

Bansilal, S., Brijlall, D., & Trigueros, M. (2017). An APOS Study on Pre-service Teachers’ Understanding of Injections and Surjections. Journal of Mathematical Behavior, 48, 22–37. https://doi.org/10.1016/j.jmathb.2017.08.002

Baye, M. G., Ayele, M. A., & Wondimuneh, T. E. (2021). Implementing GeoGebra Integrated with Multi-teaching Approaches Guided by the APOS Theory to Enhance Students’ Conceptual Understanding of Limit in Ethiopian Universities. Heliyon, 7, 1–13. https://doi.org/10.1016/j.heliyon.2021.e07012

Bikner-Ahsbahs, A., & Prediger, S. (2014). Networking of Theories as a Research Practice in Mathematics Education. Switzerland: Springer. https://doi.org/10.1007/978-3-319-05389-9

Borji, V., & Font, V. (2019). Exploring Students’ Understanding of Integration by Parts: A Combined Use of APOS and OSA. EURASIA: Journal of Mathematics, Science and Technology Education, 15(7), 1–13. https://doi.org/10.29333/ejmste/106166

Borji, V., & Martínez-Planell, R. (2023). On Students’ Understanding of Volumes of Solids of Revolution: An APOS Analysis. Journal of Mathematical Behavior, 70, 1–20. https://doi.org/10.1016/j.jmathb.2022.101027

Borji, V., Alamolhodaei, H., & Radmehr, F. (2018). Application of the APOS-ACE Theory to Improve Students’ Graphical Understanding of Derivative. EURASIA Journal of Mathematics, Science and Technology Education, 14(7), 2947–2967. https://doi.org/10.29333/ejmste/91451

Bressoud, D. M. (2021). The Strange Role of Calculus in the United States. ZDM–Mathematics Education, 53(3), 521–533. https://doi.org/10.1007/s11858-020-01188-0

Bressoud, D., Burn, H., Hsu, E., Mesa, W., Rasmussen, C., & White, N. (2014). Successful Calculus Programs: Two-year Colleges to Research Universities. USA: NCTM.

Brijlall, D., & Ndlazi, N. J. (2019). Analyzing Engineering Students’ Understanding of Integration to Propose a Genetic Decomposition. Journal of Mathematical Behavior, 55, 1–12. https://doi.org/10.1016/j.jmathb.2019.01.006

Burgos, M., Bueno, S., Godino, J. D., & Pérez, O. (2021). Onto-semiotic Complexity of the Definite Integral: Implications for Teaching and Learning Calculus. REDIMAT – Journal of Research in Mathematics Education, 10(1), 4–40. https://doi.org/10.17583/redimat.2021.6778

Chapell, K. K., & Kilpartrick, K. (2003). Effects of Concept-based Instruction on Students’ Conceptual Understanding and Procedural Knowledge of Calculus. PRIMUS, 13(1), 17–37. https://doi.org/10.1080/10511970308984043

Cline, K., Parker, M., Zullo, H., & Stewart, A. (2013). Addressing Common Student Errors with Classroom Voting in Multivariable Calculus. PRIMUS, 23(1), 60–75. https://doi.org/10.1080/10511970.2012.697098

Díaz-Berrios, T., & Martínez-Planell, R. (2022). High School Student Understanding of Exponential and Logarithmic Functions. Journal of Mathematical Behavior, 66, 1–20. https://doi.org/10.1016/j.jmathb.2022.100953

Dominguez, A., Barniol, P., & Zavala, G. (2017). Test of Understanding Graphs in Calculus: Test of Students’ Interpretation of Calculus Graphs. EURASIA Journal of Mathematics, Science and Technology Education, 13(10), 6507–6531. https://doi.org/10.12973/ejmste/78085

Dubinsky, E. (2013). Using a Theory of Learning in College Mathematics Courses. MSOR Connections, 1(2), 10–15.

Ergene, Ö. & Özdemir, A. Ş. (2020). Investigating Pre-service Elementary Mathematics Teachers’ Perception of Integral. Journal of Educational Sciences, 51(51), 155–176. https://doi.org/10.15285/maruaebd.622149

Ergene, Ö. (2014). Investigation of Personal Relationship in Integral Volume Problems Solving Process within Communities of Practices. Dissertation. Marmara University.

Ergene, Ö., & Özdemir, A. Ş. (2022). Understanding the Definite Integral with the Help of Riemann Sums. Participatory Educational Research, 9(3), 445–465. https://doi.org/10.17275/per.22.75.9.3

Fernandez, A., & Mohammed, P. (2021). Hermite‐Hadamard Inequalities in Fractional Calculus Defined Using Mittag‐Leffler Kernels. Mathematical Methods in the Applied Sciences, 44(10), 8414–8431. https://doi.org/10.1002/mma.6188

Ferrini-Mundi, J., & Graham, K. (1994). Research in Calculus Learning: Understanding of Limits, Derivatives and Integrals. In J. J. Kaput & E. Dubinsky (eds.), Research Issues in Undergraduate Mathematics Learning, (pp.31–45). Washington DC: MAA.

Figueroa, A. P., Possani, E., & Trigueros, M. (2017). Matrix Multiplication and Transformations: An APOS Approach. Journal of Mathematical Behavior, 1–15. https://doi.org/10.1016/j.jmathb.2017.11.002

Font, V., Trigueros, M., Badillo, E., & Rubio, N. (2016). Mathematical Objects through the Lens of Two Different Theoretical Perspectives: APOS and OSA. Educational Studies in Mathematics, 91(1), 107–122. https://doi.org/10.1007/s10649-015-9639-6

Frank, K., & Thompson, P. W. (2021). School Students’ Preparation for Calculus in the United States. ZDM–Mathematics Education, 53(3), 549–562. https://doi.org/10.1007/s11858-021-01231-8

García-Martínez, I., & Parraguez, M. (2017). The Basis Step in the Construction of the Principle of Mathematical Induction Based on APOS Theory. Journal of Mathematical Behavior, 46, 128–143. https://doi.org/10.1016/j.jmathb.2017.04.001

Harel, G. (2017). The Learning and Teaching of Linear Algebra: Observations and Generalizations. The Journal of Mathematical Behavior, 46, 69–95. https://doi.org/10.1016/j.jmathb.2017.02.007

Hong, D. S., Choi, K. M., Hwang, J., & Runnalls, C. (2017). Integral Students’ Experiences: Measuring Instructional Quality and Instructors’ Challenges in Calculus 1 Lessons. International Journal of Research in Education and Science, 3(2), 424–437. https://doi.org/10.21890/ijres.327901

Kiat, S. E. (2005). Analysis of Students’ Difficulties in Solving Integration Problems. The Mathematics Educator, 9(1), 39–59.

Lam, T. T., Guan, T. E., & Luen, T. C. (2021). Fallacies About the Derivative of the Trigonometric Sine Function. The Mathematician Educator, 2(1), 1–10.

Li, V. L., Julaihi, N. H., & Eng, T. H. (2017). Misconceptions and Errors in Learning Integral Calculus. Asian Journal of University Education, 13(1), 17–39. https://ir.uitm.edu.my/id/eprint/21914

Maharaj, A. (2014). An APOS Analysis of Natural Science Students’ Understanding of Integration. REDIMAT – Journal of Research in Mathematics Education, 3(1), 54–73. https://doi.org/10.4471/redimat.2014.40

Mahir N. (2009). Conceptual and Procedural Performance of Undergraduate Students in Integration. International Journal of Mathematical Education in Science and Technology, 40(2), 201–211. https://doi.org/10.1080/00207390802213591

Marsitin, R. (2017). Koneksi Matematis dan Berpikir Kreatif dalam Pembelajaran Matematika dengan Teori APOS [Mathematical Connection and Creative Thinking in Mathematics Learning with APOS Theory]. Al-Khwarizmi: Jurnal Pendidikan Matematika dan Ilmu Pengetahuan Alam, 5(1), 87–100. https://doi.org/10.24256/jpmipa.v5i1.268

Martínez-Planell, R., & Trigueros, M. (2019). Using Cycles of Research in APOS: The Case of Functions of Two Variables. Journal of Mathematical Behavior, 55, 1–22. https://doi.org/10.1016/j.jmathb.2019.01.003

Martínez-Planell, R., & Trigueros, M. (2020). Students’ Understanding of Riemann Sums for Integrals of Functions of Two Variables. Journal of Mathematical Behavior, 59, 1–26. https://doi.org/10.1016/j.jmathb.2020.100791

Martínez-Planell, R., & Trigueros, M. (2021). Multivariable Calculus Results in Different Countries. ZDM – Mathematics Education, 53, 695–707. https://doi.org/10.1007/s11858-021-01233-6

Martínez-Planell, R., Trigueros, M., & Borji, V. (2022). The Relation Between Riemann Sums and Double Integrals: Results of a Second Research Cycle. Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education, 3, 179–186. http://hdl.handle.net/10045/126627

Mateus, E. (2016). Teaching Analysis to Process Integration Method Instruction by Parties. Bolema: Boletim de Educação Matemática, 30(55), 559–585. https://doi.org/10.1590/1980-4415v30n55a13

McGee, D., & Martínez-Planell, R. (2014). A Study of Semiotic Registers in the Development of the Definite Integral of Functions of Two and Three Variables. International Journal of Science and Mathematics Education, 12(4), 883–916. https://doi.org/10.1007/s10763-013-9437-5

Metaxas, N. (2007). Difficulties on Understanding the Indefinite Integral. In Woo, J. H., Lew, H. C., Park, K. S., Seo, D. Y. (Eds.). Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, 3, 265–272.

Miller, R. L., Santana-Vega, E., & Terrell, M. S. (2006). Can Good Questions and Peer Discussion Improve Calculus Instruction? PRIMUS, 16(3), 193–203. https://doi.org/10.1080/10511970608984146

Misu, L., Budayasa, I. K., Lukito, A., Hasnawati., & Rahim, U. (2019). Profile of Metacognition of Mathematics Education Students in Understanding the Concept of Integral in Category Classifying and Summarizing. International Journal of Instruction, 12(3), 481–496. https://doi.org/10.29333/iji.2019.12329a

Nagle, C., Martínez-Planell, R., & Moore-Russo, D. (2019). Using APOS Theory as a Framework for Considering Slope Understanding. Journal of Mathematical Behavior, 54, 1–14. https://doi.org/10.1016/j.jmathb.2018.12.003

Newman, M. A. (1977). An Analysis of Sixth-grade Pupils’ Error on Written Mathematical Tasks. Victorian Institute for Educational Research Bulletin, 39, 31–43. https://cir.nii.ac.jp/crid/1573105976160816128

Oktaç, A., Trigueros, M., & Romo, A. (2019). APOS Theory: Connecting Research and Teaching. For the Learning of Mathematics, 39(1), 33–37. https://www.jstor.org/stable/26742010

Orton, A. (1983). Students’ Understanding of Integration. Educational Studies in Mathematics, 14(1), 1–18. https://doi.org/10.1007/BF00704699

Pepper, R., Stephanie, V. C., Steven J. P., & Katherine K. P. (2012). Observations on Student Difficulties with Mathematics in Upper-division Electricity and Magnetism. Physical Review Special Topics – Physics Education Research, 8(1), 1–15. https://doi.org/10.1103/PhysRevSTPER.8.010111

Perfekt, K. M. (2021). Plasmonic Eigenvalue Problem for Corners: Limiting Absorption Principle and Absolute Continuity in the Essential Spectrum. Journal de Mathématiques Pures et Appliquées, 145, 130–162. https://doi.org/10.1016/j.matpur.2020.07.001

Rasslan, S., & Tall, D. (2002). Definitions and Images for the Definite Integral Concept. Proceedings of the 26th PME, 4, 89–96.

Seah, E. K. (2005). Analysis of Students’ Difficulties in Solving Integration Problems. The Mathematics Educator, 9(1), 39–59.

Sealey, V. (2008). Calculus Students’ Assimilation of the Riemann Integral into a Previously Established Limit Structure. Dissertation. Arizona State University.

Şefik, Ö., & Dost, Ş. (2020). The Analysis of the Understanding of the Three-dimensional (Euclidian) Space and the Two-variable Function Concept by University Students. Journal of Mathematical Behavior, 57, 1–19. https://doi.org/10.1016/j.jmathb.2019.03.004

Sholihah, U., & Maryono. (2020). Students’ Visual Thinking Ability in Solving the Integral Problem. Journal of Research and Advances in Mathematics Education, 5(2), 175–186. https://doi.org/10.23917/jramathedu.v5i2.10286

Siyepu, S. W. (2015). Analysis of Errors in Derivatives of Trigonometric Functions. International Journal of STEM Education, 2(16), 1–16. https://doi.org/10.1186/s40594-015-0029-5

Sofronas, K. S. (2011). What does it Mean for a Student to Understand the First-year Calculus? Perspectives of 24 Experts. The Journal of Mathematical Behavior, 30(2), 131–148. https://doi.org/10.1016/j.jmathb.2011.02.001

Swan, M. (2001). Dealing with Misconceptions in Mathematics. In Gates, P. (Ed.), Issues in Mathematics Teaching, (pp. 147–165). London: Routledge Falmer.

Syamsuri., & Santosa, C. (2021). Thinking Structure of Students’ Understanding of Probability Concept in Term of APOS Theory. MaPan: Jurnal Matematika dan Pembelajaran, 9(1), 119–135. https://doi.org/10.24252/mapan.2021v9n1a8

Syarifuddin, A., & Sari, A. F. (2021). Misconceptions of Prospective Mathematics Teacher on Graphing Function. Journal of Physics: Conference Series, 1869(1), 1–6. https://doi.org/10.1088/1742-6596/1869/1/012115

Tall, D. (1985). Understanding the Calculus. Mathematics Teaching, 110, 49–53.

Tall, D. (2011). Looking for the Bigger Picture. For the Learning of Mathematics, 31(2), 17–18.

Tall, D. (2014). Making Sense of Mathematical Reasoning and Proof. In Fried, M., Dreyfus, T. (Ed)., Mathematics & Mathematics Education: Searching for Common Ground, (pp. 223–235). New York: Springer. https://doi.org/10.1007/978-94-007-7473-5_13

Talley, J. R. (2009). Calculus Instructors’ Responses to Prior Knowledge Errors. Dissertation. University of Oklahoma, United States.

White, P., & Mitchelmore, M. (1996). Conceptual Knowledge in Introductory Calculus. Journal for Research in Mathematics Education, 27(1), 79–95. https://doi.org/10.5951/jresematheduc.27.1.0079

Wibawa, K. A., Nusantara, T., Subanji., & Parta, I. N. (2017). Fragmentation of Thinking Structure’s Students to Solving the Problem of Application Definite Integral in Area. International Education Studies, 10(5), 48–60. https://doi.org/10.5539/ies.v10n5p48

Zullo, H., Cline, K., Parker, M., Buckmire, R., George, J., Gurski, K., Larsen, J., Mellor, B., Oberweiser, J., Peterson, D., Spindler, R., Stewart, A., & Storm, C. (2011). Student Surveys: What do They Think? Mathematical Association of America, 29–34. https://doi.org/10.1017/CBO9781614443018.006

Zwanch, K. (2019). A Preliminary Genetic Decomposition of Probabilistic Independence. The Mathematics Educator, 28(1), 3–26. https://files.eric.ed.gov/fulltext/EJ1225414.pdf

Analysis of Concept Construction and Student Errors on the Topic of Double Integral Based on APOS Theory

Article Sidebar

Main Article Content

Abstract

Keywords

Article Details

References

References

Similar Articles